© Prof. Dr. Knut Barghorn, Jade Hochschule. Studienort WHV. E-mail: knut.barghorn@jade-hs.de

1. Zahlensysteme und Arithmetik

1.1 Lernziele, Literaturtipps und URLs

Ziel dieser Einheit

Wir werden in diesem Kapitel lernen, dass es nicht nur das bekannte Dezimalsystem gibt, mit dem Sie seit der ersten Schulklasse rechnen. Wir werden uns historisch an das Thema annähern und andere Systeme ansehen. Wir werden das Dualsystem und das Hexadezimalsystem kennen lernen. Wir werden lernen, Werte der verschiedenen Zahlensysteme ineinander zu überführen. Danach werden wir lernen, wie mit dem Dualsystem gerechnet werden kann. Wir werden die Grundrechenarten (Addition, Subtraktion, Multiplikation und Division) auf das Dualsystem anwenden lernen. Nebenbei werden wir verstehen, warum das Dualsystem und auch das Hexadezimalsystem gerade für die Informatik so wichtig sind. Anschließen werden wir uns noch kurz mit Codes beschäftigen, um zu verstehen, dass es in der Ablage von Speicherinformation notwendig ist, die Information richtig zuzuordnen.

Literaturtipps

• Lothar Moos, "Zahlensysteme", Publicis Corporate Publishing; ca.15 EUR, Für Einsteiger gut geeignet
• Heinz-Peter Gumm, "Einführung in die Informatik", Oldenbourg; 39,80 EUR, Gutes Einsteigerbuch für Anfänger in der Informatik generell.
• Dieses Skript, 0,00 EUR, Für die Klausur ausreichend
• Das Internet, "Google-Suche: "Zahlensysteme" oder "Codes", 0,00 EUR, Es gibt zu dem Thema einige gute Seiten im Internet.

1.2 Historie der Zahlensysteme

Zahlensysteme gibt es bereits seit einiger Zeit. Die ersten Systeme zur Zählung lassen sich auf 30.000 vor Chr. datieren. Es wurden  Mammutknochen gefunden, in die Zählkerben eingeritzt waren. (Quelle: Ifrah, Georges: Universalgeschichte der Zahlen)

Um 15.000 vor Chr. gibt es die ersten Tontafeln mit Zahlzeichen für Hammel und Ziegen (ebenfalls aus Ifrah)

Nun machen wir einen kleinen geschichtlichen Sprung auf der Zeittafel.

Die Römer begannen ab dem fünften Jahrhundert v. Chr. die Darstellung von Zahlen durch Zahlzeichen, die dem westgriechischen Alphabet entliehen waren. Der genaue Ursprung dieser Form des Additionssystems konnte allerdings bis heute nicht vollständig geklärt werden. Sicher ist jedoch, dass römische Zahlenzeichen eine Abwandlung erheblich älterer Zeichen sind und alternativ zu Kerbzeichen zuerst zum Zählen von Menschen, Vieh, Geld und Hausrat verwendet wurden; also um damit festzustellen, welche Menge mehr Bestandteile hat.

Die römischen Zahlen sind sicherlich bekannt.

Die Darstellung von Werten zwischen den Hauptwerten wurden additiv durch die Darstellung von mehreren Zeichen erreicht.

In der dritten Zeile entdecken Sie die Darstellung von 14. Zunächst war es bei den Römern üblich die Zeichen rein additiv zu nutzen. Erst ab die Mittelalter ging man dazu über, die vorangestellten kleineren Werte von den folgenden größeren Werten zu subtrahieren. 

Beispiel:

Die Ableitung dieses Zahlensystems kann man sich aus der Verwendung des Fingersystems vorstellen. Die I stellen einen Finger dar. Die V eine ganze Hand voll Finger (5) und das X zwei volle Hände.

Das System war nicht mit einen Schlag voll erfunden, sondern hat sich vermutlich entwickelt. Wie Isidor von Sevilla um 620 n. Chr. in seiner zwanzigbändigen Enzyklopädie des gesamten Wissens jener Zeit » Originum seu etymologiarum libri XX « berichtet, soll der Dichter Quintus Ennius (geboren 239 v. Chr. in Rudiae, Kalabrien, gestorben 169 v. Chr.) die beiden Darstellungen M für Mille (Tausend) und C für Centum (Hundert) erfunden haben.

Das Rechnen mit den Fingern war sicherlich einfach ableitbar und begründet die Darstellung von 5 und 10 als besondere Zeichen, aber es wurden auch noch andere Systeme gefunden. Beobachten Sie einmal Schulanfänger. Sie werden feststellen, dass diese noch mit den Fingern rechnen, obwohl es Ihnen nicht beigebracht wurde. Kinder finden sehr schnell heraus, dass eine Hand fünf Finger hat und sich dieser Sachverhalt nicht ändert, also nicht immer wieder nachgezählt werden muss.

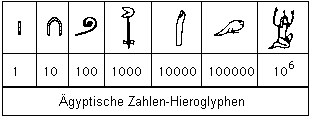
Die Ägypter verwendeten ein sehr ähnliches Zahlensystem. Hier finden sich die Zeichen ebenfalls in 10er Potenzen dargestellt.

Sie nutzten Sie die Zeichen ebenfalls additiv in der Darstellung:

Quelle der beiden Bilder: http://home.fonline.de/fo0126/geschichte/ges1.htm

Das Zahlensystem der Maya (um 250 n. Chr.) operiert mit nur 3 Symbolen: einer stilisierten Muschel für Null oder Vollendung, einen Punkt für 1 und einen Strich für 5. Die Basis war 20 (und nicht 10 wie bei uns). Sie ordneten die Zahlen vertikal an, mit den niedrigsten Werten unten und den höchsten an der Spitze.

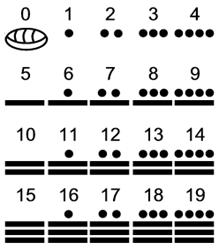
Quelle: http://www.indianer-wiki.org/Maya-Ziffern

Die Basis des Zahlensystems der Maya ist nicht 10 (wie bei den Römern oder Ägyptern), sondern 20. Die Ableitung erfolgte wahrscheinlich unter zu Hilfenahme der Zehen an den Füßen.

Wenn die Mayas Zahlen größer der 20 darstellen wollten, taten Sie dieses indem Sie Blöcke von 20er untereinander schrieben.

Die unterste Ebene stellt die Zahl 7 dar. Die Ebene darüber die 12*20=240, die nächst höhere die 9*20*20=3600. Insgesamt wird also die Zahl 7+240+3600=3847 dargestellt.

Das Besondere des Maya-Zahlensystems war aber die Verwendung der Null, die man bei der Darstellung der derzeit aktuellen Jahreszahl ebenfalls benötigt. Die Null wa bei den Römern gänzlich unbekannt.

All diesen Zahlensystemen ist eines gemeinsam. Die Darstellung macht ein Rechnen außerordentlich schwierig. Stellen Sie sich vor, Sie sollen die Zahlen MCLX und XCVII miteinander multiplizieren. Versuchen Sie es, aber nehmen Sie bitte nicht das bekannte heutige Zahlensystem zu Hilfe.

Unser heutiges Zahlensystem kam erst im 12. Jahrhundert über die Araber nach Europa. Es stammt ursprünglich aus Indien. In diesem hindu-arabischen Zahlensystem gab es die Null schon seit tausend Jahren.

Aufgabe zur Mitarbeit: : Stellen Sie die aktuelle Jahreszahl im Maya-Zahlensystem dar.

1.3 Das Dezimalsystem

Das heute verwendete Zahlensystem ist ein Stellenwertsystem oder auch Positionssystem. Das Besondere daran ist, dass der Zahlenwert von der Position der Ziffer innerhalb einer Zahl abhängig ist.

Vorsicht: Die Bedeutung der Worte "Zahl" und "Ziffer" unterscheidet sich deutlich. Eine Ziffer ist ein diskreter Einzelwert (im Dezimalsystem z.B. 2 oder 3 oder 8...), die Zahl ist eine Zusammenstellung von Ziffern, in deren Ergebnis je nach Bildungsgesetz ein konkreter Wert repräsentiert wird (z.B. 367).

Beispiel: Die Zahl 3735

Die erste Ziffer entspricht dem Wert 3000	Stellengewicht 1000	=10³
Die zweite Ziffer entspricht dem Wert 700	Stellengewicht 100	=10²
Die dritte Ziffer entspricht dem Wert 30	Stellengewicht 10	=10¹
Die vierte Ziffer entspricht dem Wert 5	Stellengewicht 1	=100

Den Wert einer dargestellten Zahl erhält man also, wenn man die

Werte aller Ziffern mit ihren Stellengewichten multipliziert und die Produkte addiert.

Beispiel: 3*10³+7*10²+3*10¹+5*10⁰ = 3*1000+7*100+3*10+5*1 = 3000+700+30+5 = 3735

Wenn wir diese Vorschrift formalisieren und in eine mathematische Form bringen, schreiben wir folgendes:

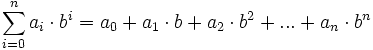
So lässt sich jede Zahl bezüglich einer Basis b eindeutig durch die Ziffern a darstellen.

Unser heutiges System (das Dezimalsystem) hat die Basis 10 (wie wir gerade gesehen haben). Auch das System der Maya war ein Stellenwertsystem Die Mayas verwendeten die Basis 20. Das Zahlensystem der Mayas nennt man deshalb auch Vigesimalsystem.

Eigenschaften von Stellenwertsystemen sind:

• Es gibt eine Ziffer mit dem Wert Null
• Verschiebung um eine Position entsprechen einer Multiplikation oder Division mit der Basis b

Aufgabe : Nennen Sie ein Zahlensystem, das kein Stellenwertsystem ist. Zahlensysteme, die kein Stellenwertsystem darstellen nennt man übrigens Ziffernwertsysteme!

Weitere Stellenwertsysteme mit verschiedenen Basen sind:

b=2 : Dualsystem (Ziffern: 0,1)

b=8: Oktalsystem (Ziffern: 0,1,2,3,4,5,6,7)

b=16: Hexadezimalsystem (Ziffern: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)

1.4 Das Dualsystem

Wie wir gerade gesehen haben, ist das Dualsystem ein Stellenwertsystem zur Basis b=2. Zur Darstellung werden die Werte 0 und 1 verwendet.

Gerade in technischen Bereichen wird dieses System häufig verwendet. Bei Schaltungen lassen sich die Werte 0 und 1 leicht darstellen in Form von „ist nicht da“ oder „ist da“. So lässt sich beispielsweise ein Strom anlegen oder auch nicht, ein Lichtimpuls feststellen oder auch nicht, oder ein Kratzer auf einer ansonsten glatten Oberfläche ausmachen. 

Gerade für die Informatik ist damit dieses System sehr wichtig, da die Zahlen in Computern im Dualsystem dargestellt werden. Die Stelle einer Dualzahl nennt man Bit. Acht Bit (Bit steht für Binary digit, engl. kleiner Happen) sind ein Byte.

Dabei kommt die Zahl 8 nicht von ungefähr, denn jedes druckbare Zeichen kann man mit 8 bit darstellen.

8 bit in Binärschreibweise können einen dezimalen Maximalwert von
11111111 = 255 (= 256 Einzelwerte, da die 0 mitgerechnet wird) annehmen.

Die ersten 8-bit-PC hatten eine interne Verarbeitungsbreite von eben diesen 8 bit, d.h., dass der Prozessor maximal Zahlen von 255 direkt verarbeiten kann, größere Zahlen musste er erst mühselig aus "Einzelteilen" zusammensetzen, seine Berechnungen durchführen und anschließend wieder zerteilen, um sie auf dem 8 bit breiten Datenbus an den jeweiligen Empfänger zu schicken. Man kann leicht beurteilen, welchen Geschwindigkeitszuwachs heutige 32-bit-Rechner bringen.

Werden 8 bit zu einer Einheit zusammengefasst, erhält man 1 Byte - dies ist die kleinste adressierbare Informationseinheit in der EDV.

1101 0011 0110 1100 diese Zahl besteht also aus 2 Byte

Die größte darstellbare Zahl mit einem Byte ist also 255. Benötigt man auch negative Zahlen, kann man im einfachsten Fall das erste bit als Vorzeichen (0 bedeutet positiv, 1 negativ) verwenden und man kann mit den verbleibenden 7 bit noch Zahlen realisieren von -127 bis +127 (die 0 gibt es 2-mal, positiv und negativ).

Werden bit und Byte als Abkürzungen verwendet, z.B. in Kilobit oder Kilobyte, ist es allgemein üblich, zur besseren Unterscheidung für bit ein kleines b und für Byte ein großes B zu verwenden (5 kB = 5 KiloByte).

Ein Beispiel für die Umwandlung eines Werte im Dualsystems in das Dezimalsystem werden wir nun durchrechnen:

Gegeben sei der Wert 101010

Der Wert 101010 zur Basis 2 entspricht also dem Wert 0+2+0+8+0+32=42 im Dezimalsystem.

1.5 Das Hexadezimalsystem

Für Zahlenangaben ist die Darstellung in Binärschreibweise sehr umständlich und unübersichtlich. Schon eine 5-stellige Dezimalzahl würde binär 16 Stellen benötigen! Aus diesem Grunde hat man sich für reine Darstellungszwecke für ein Zahlensystem mit größerem Ziffernumfang entschieden.

Es fällt uns zwar etwas schwer, aus unserem dezimalen Denken auszubrechen und hexadezimal zu denken, da wir Probleme haben, die Ziffern oberhalb von 9 darzustellen. Eine 10 zu schreiben ist nicht erlaubt, sie erinnern sich bitte an den Unterschied zwischen Ziffern und Zahlen. 10 als Zahl im Hexadezimalen bedeutet 16 im Dezimalsystem. Man verwendet deshalb Buchstaben und fängt bei A für die dezimale 10 an. Die größte im hexadezimalen System darstellbare Ziffer entspricht der dezimalen Zahl 15. Wenn wir das Alphabet weitergehen, landen wir bei F für 15.

Ziffernvorrat hexadezimal:

0 1 2 3 ....7 8 9 A B C D E F

Groß- oder Kleinschreibung der Buchstaben spielt keine Rolle, jedoch hat sich als guter Stil die Großschreibung eingebürgert. Das allgemeine Bildungsgesetz hat auch hier seine Gültigkeit.

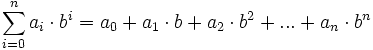
Beispiel: Ein Beispiel für dieses System ist die Darstellung eines Wertes F2A3

Die Berechnung der zugehörigen Darstellung im Dezimalsystems erfolgt wieder nach der obigen Regel:

Damit ist der Wert F2A3 zur Basis 16 äquivalent zum Wert 61440+512+160+3=62115 zur Basis 10.

Nun mögen Sie fragen, warum gerade die Hexadezimalzahlen für die Darstellung großer Zahlen in der EDV übersichtlicher sind als die Dualzahlen

Eine Ziffer hex kann maximal den dezimalen Wert 15 annehmen. Bezogen auf das Binärsystem entspricht das 4 bit (1111 bin = 15 dez), also genau einem Halbbyte.

Man kann also ein Byte binär mit genau 2 Ziffern hexadezimal darstellen. Diese Darstellungsweise lässt sich visuell sehr schnell erfassen und man braucht auch keine komplizierten Umrechnungsprogramme.

Beispiel:

Sieht man z.B. die Hexzahl "FF", kann man auf den ersten Blick erkennen, dass es sich hier um genau 1 Byte handelt, in dem alle bit auf 1 gesetzt sind und dies der größten darstellbaren Dezimalzahl mit einem Byte entspricht, also 255.

Nun liefere ich Ihnen eine Tabelle, die Sie sich sehr genau einprägen sollten. Die Darstellung der Dualzahlen als Hexadezimalziffern.

Beachte: es gibt keine Hexadezimalrechner. Alle Rechner rechnen ausschließlich im Dualsystem. Das Hexadezimalsystem dient lediglich zur übersichtlicheren Darstellung der Werte. Die Darstellung im Hexadezimalsystem ist bei Rechnern üblich, aber es gibt auch Rechner früherer Zeit, die die Darstellung im Oktalsystem (Basis 8) vornahmen.

1.6 Umwandlungen

Umwandlungen von Dualzahlen in Hexadezimalzahlen

Die beiden Zahlensysteme sind eng miteinander verwandt. Da sich mit vier Bit der Wertebereich einer Hexadezimalziffer abgedeckt werden kann, können diese einfach transformiert werden. (2⁴ = 16).

Verständlicher wird es an einem Beispiel:

Wir wollen die Dualzahl 110011101 in eine Hexadezimalzahl umwandeln.

Dazu teilen wir die Dualzahl in 4Bit-Blöcke (sogenannte Tetraden) auf:

1 1001 1101

Nun steht vorne eine einzelne Dualziffer. Wir füllen den Rest mit Nullen auf:

0001 1001 1101

Jedem dieser 4Bit-Blöcke ordnen wir nun sehr einfach die entsprechende hexadezimale Ziffer zu:  1  9  D.

Im Hexadezimalsystem steht für die dezimale 13 ein D.

Der Wert der Dualzahl 110011101  im Hexadezimalsystem lautet also 19D.

Aufgabe : Bitte berechnen Sie zu Hause, ob diese Darstellung auch stimmt. Dazu wandeln Sie beide Zahlen in das Dezimalsystem und vergleichen die Werte.

Umwandlung von Dezimalzahlen in Dualzahlen und Hexadezimalzahlen

Wir haben immerhin schon geschafft, Dualzahlen in Dezimalzahlen zu wandeln. Das war aber vergleichsweise einfach. Der nun folgende Part ist etwas komplizierter. Als Motivation kann ich Ihnen aber mit auf den Weg geben, dass Sie das Umrechnungsverfahren auch bei Dezimalzahlen in Hexadezimalzahlen verwenden können.

Wenn Sie die dezimale Zahl 3467 als Dualzahl darstellen wollen, können Sie natürlich die Potenzen von 2 hochzählen und die Restwerte entsprechend zerlegen. Im Dualsystem traue ich Ihnen das sogar im Kopf zu. Bei großen Dezimalzahlen, die wir als Zahlen zu einer Basis von 16 (also Hexadezimalsystem) darstellen wollen, wird das entsprechend schwieriger.

Es gibt ein mathematisches Verfahren (Restwertverfahren), das wir auf dieses Problem anwenden können.

Eine Dezimalzahl D soll in eine Zahl des y-Systems gewandelt werden:

Es sind mehrere Schritte erforderlich, bis sich ein errechneter Rest nicht mehr durch y teilen lässt
(d.h. Null ist).

D mod y = a1

(D/y) mod y = a2

((D/y)/y) mod y = a3

…

usw. bis der Ausdruck Null ergibt. Danach werden die Ergebnisse in umgekehrter Folge aneinandergereiht:

D=a3a2a1

Ich sehe Unverständnis in Ihren Gesichtern, was daran liegt, dass ich noch nicht erklärt habe, was mod bedeutet.

mod steht für den Rest der ganzzahligen Division, d.h. als a1, a2 usw. steht nicht das Divisionsergebnis sondern lediglich der Rest, der bei der Division entsteht.

Man kann das aber auch einfacher darstellen, indem wir die Vorschrift schrittweise aufschreiben:

·        Teile die Dezimalzahl D ganzzahlig durch y und schreibe den Restwert auf

·        Teile den Quotienten des vorherigen Schrittes ganzzahlig durch y und schreibe den Restwert auf

·        Fahre damit solange fort, bis der Quotient Null ergibt.

·        Schreibe die Restwerte in umgekehrt erhaltener Reihenfolge hintereinander.

Noch klarer wird es an einem Beispiel:

Gegeben sei die Dezimalzahl 42 (die kennen wir schon als Dualzahl). Wir wollen diese in das Dualsystem überführen (y=2)

D=42, y=2

42 / 2 = 21            Rest 0 (a1)

21 /2   = 10           Rest 1 (a2)

10 / 2  = 5             Rest 0 (a3)

5 / 2 = 2                Rest 1 (a4)

2 / 2 = 1                Rest 0 (a5)

1 / 2 = 0                Rest 1 (a6)

Die Dualzahl lautet also D=a6,a5,a4,a3,a2,a1 ->101010.

Wie ich schon erwähnte funktioniert das Verfahren auch mit beliebigen anderen Stellenwertsystemen.

Wie nehmen ein weiteres Beispiel zur Kontrolle:

Die dezimale Zahl 365 soll als Hexadezimalzahl ausgegeben werden:

365 / 16 = 22       Rest  13

22 / 16 = 1            Rest  6

1 / 16 = 0              Rest 1

 Die gesuchte Hexadezimalzahl lautet also 16D (für die 13 müssen wir natürlich die Ziffer D schreiben)

Aufgabe zur Mitarbeit: Wandeln Sie die Dezimalzahl 2635 in eine Hexadezimalzahl um.
Wandeln Sie die Dezimalzahl 102 in eine Dualzahl um.

Besonderheiten / Merkwürdigkeiten

Sie haben sich sicherlich auch schon darüber gewundert, dass Ihr Rechner zu Hause beim Testen des Hauptspeichers weiter zählt als Sie erwarten. Sie haben sich den neuen Rechner aus dem Supermarkt besorgt und wissen laut der Werbung, dass er über (beispielsweise, weil es sich einfach rechnen läßt) 32MB Hauptspeicher verfügt.

Die Nutzung von Vorsätzen wie Kilo, Mega, Giga ist in der Datenverarbeitung etwas eigenartig. Es ist nämlich ein KB (KByte, Kilobyte) nicht wie erwartet gleich 1000 Byte. Schuld daran ist das binäre Zahlensystem.

Im Dezimalsystem entspricht die Vorsilbe ein Kilo dem Wert 10³ . Im Dualsystem können wir die 10 als Basis aber nicht verwenden. Da hier die Basis 2 verwendet wird, suchte man nach einem Wert, der etwa der 10³ im Dezimalsystem entspricht. Am besten trifft das Ergebnis 2¹⁰

Näher kommt man nicht an die 1000 im Dezimalsystem heran, so dass man tatsächlich ansetzt:

1 KB = 2¹⁰ Byte = 1024 Byte

Gleiches gilt natürlich auch beim Megabyte. Indem man das Kilo wieder mit 1024 zu multipliziert:

1 MB = 1 KB * 1 KB = (2¹⁰ * 2¹⁰) Byte = 2²⁰ Byte = 1.048.576 Byte

analog für das Gigabyte:

1 GB = 1 KB * 1 MB = (2¹⁰ * 2²⁰) Byte = 2³⁰ Byte = 1.073.741.824 Byte

Zu beachten sind noch die Schreibweisen der Abkürzungen:

• B = Byte ; b = bit

• KB oder KByte = KiloByte (1024 Byte)

• kB oder kByte = KiloByte (1000 Byte), seltener und nicht konsequent verwendet

• Kb oder Kbit = Kilobit (eigentlich 1024 bit, oft auch als 1000 bit verwendet)

So sollte es eigentlich verwendet werden. Aber schon bei der Darstellung vom MegaByte hat sich nur MB eingebürgert, so dass Sie keine Unterscheidung mehr treffen können, ob sich auf 1000 oder 1024 als Faktor bezogen wird. Auch an die Schreibweise der Vorsilbe Kilo halten sich die wenigsten und deshalb stellen Sie bei der Werbungsangabe Ihres neuen Rechners fest, dass er nicht exakt bis 32.000.000 bit überprüft, sondern 33.554.432 bit.

• Sie kennen verschiedene Zahlensystem
• Sie können die Begriffe Stellenwertsystem und Ziffernwertsystem richtig einordnen
• Sie wissen, welche Zahlensysteme für welche Zwecke verwendet werden
• Sie können Umrechnungen von Zahlendarstellungen eines Stellenwertsystems in ein beliebiges andere Stellenwertsystem vornehmen.

1.7 Arithmetik im Dualsystem

Wir können nun schon eine ganze Menge in den Zahlensystemen machen. Aber wir sind noch nicht in der Lage in den Zahlensystemen die einfachsten Rechnungen (Grundrechenarten) durchzuführen. Auch dieses ist letztlich gar nicht schwer, wenn man es einmal verstanden hat. Da Sie nun auch die Begriffe Bit und Byte kennen, rechnen wir nun auch mit diesen. Das bedeutet, jede Dualzahl wird nun in 8 Bit-Schreibweise dargestellt. Dies können Sie erreichen, wenn Sie eine Dualzahl nach links mit Nullen auffüllen, bis die Dualzahl insgesamt acht Stellen hat. Warum wir das hier so machen, werden Sie sehen, wenn wir zu der Darstellung von negativen Zahlen kommen.

Addition

Für die Addition zweier einstelligen Zahlen im Dualsystem benötigen Sie, wie bei addieren im Dezimalsystem, manchmal einen Übertrag.

Wenn Sie im Dezimalen die einstelligen Zahlen 6 und 7 addieren wollen, schreiben Sie unter den Strich eine 3 und über den Strich eine kleine 1 (den Übertrag). Sie wissen so, dass Sie in der nächsten Stelle einen Übertrag berücksichtigen müssen.

Bei der Addition im Dualsystem verfahren Sie genauso, Sie müssen nur wissen, was die Addition der einstelligen Zahlen für Werte und Überträge ergeben.

Für die Addition zweier einstelliger Dualzahlen Y = a + b gilt

Der Übertrag bedeutet auch hier, dass das Ergebnis nicht mehr einstellig darstellbar ist.

Ein Beispiel dazu:

Addiere die beiden Dualzahlen 01010111 und 00011010

Das Ergebnis lautet 01110001

Aufgabe zum Mitdenken: Rechnen Sie die beiden zu addierenden Dualzahlen in Dezimalzahlen um, addieren Sie diese und vergleichen das Ergebnis mit dem Ergebnis der Dualzahladdition, indem Sie das Ergebnis der Dezimalzahlrechnung in eine Dualzahl überführen.

Die Addition ist also recht einfach. Da wir uns nun aber ganz bewusst einem Rechnerspeicher von 8 Bit angepasst haben, klappt die Addition nur innerhalb eines bestimmten Wertebereiches. Normalerweise verwendet man zur Addition von ganzen Zahlen einen deutlich größeren Wertebereich, aber um einen überschaubaren Rahmen zu haben, begrenzen wir uns absichtlich auf ein Byte. Unsere größte darstellbare Zahl ist die 11111111, also dezimal 255. Was passiert nun, wenn wir eine 00000001, also 1, addieren? Es kommt tatsächlich Null (00000000) heraus.
Da 1+1=0 Übertrag 1 gibt, bekommt man als Ergebnis in Wirklichkeit nicht 00000000 sondern 00000000 Übertrag 1. Dieser letzte Übertrag kann jedoch nicht mehr in einem Byte gespeichert werden und wird deshalb ersatzlos gestrichen.
Wenn ich also immer weiter eine 1 addiere, lande ich irgendwann bei 255, danach wieder bei 0 und dann irgendwann wieder bei 255. Im 1 Byte Wertebereich zählen wir also bei der laufenden Addition von 1 immer wieder von 0-255.

Subtraktion

Die Subtraktion zweier Dualzahlen ist leider etwas komplizierter. Um eine Subtraktion durchführen zu können, benötigen wir noch zwei Begriffserklärungen:

Einerkomplement

Das Einerkomplement ist die Negation der einzelnen Ziffern der Dualzahl:

Das Einerkomplement von 11111111 ist also 00000000. Das Einerkomplement von 10110011 ist 01001100.

Zweierkomplement

Das Zweierkomplement entspricht dem Einerkomplement plus einer dualen Eins. Wir nehmen also das Einerkomplement und addieren 00000001.

Das Zweierkomplement von 10011010 ist also 01100110 (01100101 + 00000001)

Das Zweierkomplement von 00011100 wird im Einerkomplement zu 11100011, im Zweierkomplement zu 11100100

Mit dem Wissen um diese Komplemente können wir nun auch subtrahieren. Dieses wird Ihnen gleich etwas komisch vorkommen und Sie werden mich fragen, warum das so geht. Das ist aber eine komplizierte Frage auf die es auch eine komplizierte Antwort gibt. Damit wollen wir uns aber nicht beschäftigen. Es ist hier wichtig, dass Sie die Regeln anwenden können. Die Frage nach dem „Warum“ beantworte ich später einmal.

Die Regel lautet: Die Subtraktion zweier Dualzahlen erfolgt durch die Addition des Zweierkomplements.

Beispiel, für die die es nicht glauben wollen:

Wenn wir von der Dualzahl 00001010 die Dualzahl 00000101 abziehen wollen, verfahren wir folgendermaßen:

Aus 00000101 wir das Einerkomplement 11111010 und das Zweierkomplement 11111011.

Addieren wir nun nach der bekannten Regel der Addition

  00001010

+11111011

----------------

  00000101

Den letzen Übertrag konnten wir nicht mehr speichern und er entfällt damit. Wir stellen also fest dass 10-5=5 ist.

Hausaufgabe: Subtrahieren Sie verschiedene Dualzahlen voneinander. Dieses Verfahren gehört zum Grundlagenverständnis.

Wir können uns das Subtrahieren auch etwas einfacher machen und die folgenden Regeln berücksichtigen:

Für die Subtraktion zweier einstelliger Dualzahlen Y = a - b gilt:

Probieren wir dies an einem Beispiel aus:

Subtrahiere die Dualzahl 0010010 von der Dualzahl 1110101 

Das Ergebnis lautet also 1100011

Diese Regel können wir gleich bei der Division noch einmal gebrauchen.

Multiplikation

Nun werden wir multiplizieren lernen. Das schriftliche Multiplizieren von Dualzahlen funktioniert genauso wie das schriftliche Multiplizieren von Dezimalzahlen.

Dazu ein kleines Beispiel:

Wir multiplizieren die beiden Dualzahlen 00001101 und 00000101

Wie Sie sehen, ist das Multiplizieren besonders einfach, da die Teilergebnisse entweder Null sind oder den Multiplikator darstellen. Sie müssen dann nur noch die Teilergebnisse stellenrichtig aufaddieren und haben sehr schnell das Ergebnis.

Übrigens: Die Multiplikation zweier n-stelliger Dualzahlen hat die Stellenzahl 2n-1. Dieses zu wissen, macht durchaus Sinn, weil wenn wir im Rechner multiplizieren, müssen wir wieder auf den Überlauf achten.

Für die Multiplikation im Rechner gibt es eine schöne Berechnungsvorschrift. Im Rechner wird die Multiplikation durch einfache Bitverschiebung und Addition gelöst. Jeder Rechner verfügt über eine Bitverschiebungsfunktion. Man spricht auch von einem Shift

Berechnungsvorschrift zur Multiplikation zweier Dualzahlen x und y:

1.      Setze Ergebnisspeicher auf 0

2.      wenn die letzte Stelle von y = 1 ist, addiere x zum Ergebnisspeicher

3.      Verschiebe y um eine Stelle nach rechts (die in Schritt 1. behandelte Stelle wird "hinausgeschoben", sie verschwindet also).

4.      Verschiebe x um eine Stelle nach links (entspricht Multiplikation mit 2 -> wegen der stellenrichtigen Addition)

5.      Wenn y nicht 0 ist, gehe zu Schritt 2.

Die 5. Anweisung hat zur Folge, dass die Multiplikation beendet wird, sobald nichts mehr zu addieren ist. Bei einer Wortbreite von n, ist die Multiplikation auf jeden Fall nach n Schritten beendet.

Aufgabe zum Mitdenken: Multiplizieren Sie die Dualzahlen 00000110 und 000101 anhand des obigen Algorithmus

Division

Die Division ist ebenfalls recht einfach zu bewerkstelligen. Hier kommen wir wieder mit der Grundschulmathematik und dem bisherigen Wissen bequem aus.

Wir dividieren die Dualzahl 101110 durch die Dualzahl 101.

Bei der Multiplikation wird ein Links-Shift durchgeführt, dementsprechend ist es logisch, dass bei der Division ein Rechts-Shift durchgeführt wird. Teile ich die Zahl 8 durch 2 ergibt das 4, in Dualschreibweise 00001000 / 00000010 = 00000100. Die Division durch 2 entspricht also einem Rechts-Shift von einer Stelle. Die Division von 8 durch 4 ergibt 2, in Dualschreibweise 00001000 / 00000100 = 00000010, also ein Rechts-Shift von zwei Stellen. Was passiert nun aber mit Nachkommastellen?

Schauen wir uns die einfache Division von 3 durch 2 an. 00000011 / 00000010 = 00000001. Der Rechts-Shift bewirkt, dass die letzte 1 rechts aus dem Zahlenbereich "herausfällt". Das bedeutet, dass alle Nachkommastellen abgeschnitten werden. Wichtig: Es wird nicht gerundet, es wird abgeschnitten. Das Ergebnis aus 3 durch 2 ist also 1!!! Diese Art der Division funktioniert jedoch nur, wenn man durch 2 oder eine Potenz von 2 dividiert.

Sie können die vier Grundrechenarten auf das Dualsystem anwenden.

Negative Dualzahlen

Nun werden Sie sagen, das ist ja alles schön und gut, aber wie stelle ich eine negative Zahl dar? Gut werde ich sagen, kümmern wir uns jetzt auch mal darum. Wir haben bislang gesehen, dass es Dualzahlen gibt. Im Rechner werden Dualzahlen in Speicherbereichen mit festen Größen abgelegt. Wie groß dieser Speicherbereich ist, spielt dabei eigentlich keine Rolle, aber wir nehmen erst einmal an, er betrüge 8Bit = 1 Byte. Wir haben den darstellbaren Wertevorrat von 0-255 (also insgesamt 256 Zeichen).

Ein Ansatz wäre vielleicht, die negativen Zahlen einfach wie im Dezimalsystem mit einem Vorzeichen (flag) zu versehen.

Bei einer Dualzahl wäre dann zum Beispiel : 00000001 die 1 und 10000001 die -1.

Der Ansatz ist verlockend aber mathematisch nicht durchzuhalten. Wie wir wissen, führt die Addition von 00000001 zur nächst höheren Zahl. Probieren wir das einmal mit der -1 also 10000001 aus.

  10000001 + 00000001 = 10000010

In dezimaler Schreibweise steht hier nun  -1 + 1 = -2, was offensichtlich falsch ist.

Wir haben oben die Einerkomplemente und Zweierkomplemente eingeführt. Interessanterweise helfen die uns deutlich bei der Lösung:

Wenn wir das Einerkomplement als Darstellung der negativen Zahl nutzen, passiert Folgendes:

Nehmen wir die Zahl 00000101 (5), transformieren sie in das Komplement 11111010 und addieren 00000001. Es kommt die Zahl 11111011 heraus. Wenn dieses die -4 darstellt, muss das Einerkomplement  dazu ( 00000100 )  4 darstellen.

Scheint geklappt zu haben. Aber was passiert nun, wenn wir das Komplement von 00000000 also 11111111 bilden.

Unser Wertebereich hat zwei Nullen. Eine positive und eine negative Null. Das wäre je erst mal nicht problematisch, aber:

Addiere zu 1111111 eine 00000001 hinzu: (Bedenke, wir haben einen begrenzten Speicher und wenn der Überlauf droht, sollen wir wieder von vorne zu zählen beginnen.

Dummerweise ergibt 11111111 + 00000001 = 00000000 (die Übertragseins ist ja zu vernachlässigen)

Da auch diese Aussage falsch ist, müssen wir noch etwas nachbessern.

Der Ausweg stellt das Zweierkomplement dar. Wenn die negative Zahl durch das Zweierkomplement dargestellt wird, gehen alle Rechnungen wirklich auf.

Nehmen wir noch mal das Beispiel von gerade: Das Zweierkomplement von 00000000 ist 00000000. Addieren wir eine 00000001 hinzu, kommt wirklich 00000001 heraus. Die Rechnung geht auf.

Ein anderes Beispiel, damit Sie mir glauben:

Wir wollen im Dualsystem -5 + 2 rechnen. Es sollte -3 herauskommen.

00000101 stellt die 5 dar.

11111011 stellt das Zweierkomplement also die -5 dar.

11111011 + 00000010 ergibt 11111101

Die Rückrechnung aus dem Zweierkomplement ins Einerkomplement ergibt 11111101 – 00000001 = 11111100

Das Einerkomplement von 11111100 ist 00000011 also wirklich die 3.

Also stellt 11111101 tatsächlich die -3 dar.

Das Gute ist, dass immer noch am ersten Bit zu erkennen ist, ob eine Zahl positiv oder negativ ist.

Wenn wir folgende Zahlen nehmen, erkennen wir, dass sich der Wertebereich nun verschoben hat:

00000000 = 0
01111111 = 127
10000000 = -128

Wir nutzen nicht mehr den Bereich 0-255 sondern einen Bereich von -128 bis 127.

Festkommazahlen

Bislang haben wir uns immer nur um die ganzen Zahlen 2⁰ , 2¹ , 2² , … gekümmert. Nun wollen wir aber wissen, was passiert, wenn wir die Nachkommastellen ebenfalls darstellen.

Wir erweitern dazu einfach das System auf Brüche 2^-1  2^{-2 ,} 2^-3 , … rechts vom Dezimalkomma.

Beispiel: 1011,1101 stellt die Zahl 8+0+2+1+0,5+0,25+0+0,0625= 11,8125 dar.

Die Rechenoperationen (Addition, Subtraktion, Multiplikation, Division) funktionieren wie bei ganzen Zahlen.

Gleitkommazahlen

Das könnte es nun gewesen sein, denken Sie. Aber wir haben im Rechner noch ein Problem:

Die Zahlen die wir bislang behandelt haben, haben alle ein Ende. Was aber machen wir mit Zahlen, die kein Ende nehmen wollen.

Wenn Sie 10 durch 3 teilen bekommen Sie 3,3333…..

Im alltäglichen Leben geben wir uns damit zufrieden, wenn wir sagen von einem Lottogewinn von 10 Euro bekommt jeder 3,33 Euro. Den übrig gebliebenen Cent vernachlässigen wir meist.

Bei einem Rechner, der alles ziemlich genau nimmt, gibt es aber ein Problem, denn wenn wir nun mit 3,33 weiterrechnen, ergibt 3,33 * 3 = 9,99 und nicht 10. Das kann bei Berechnungen schnell zu einem Problem werden, da sich solche Rundungsfehler möglicherweise aufsummieren und im Endergebnis zu einem nicht zu vernachlässigenden Fehler führen.

Den Ausweg aus diesem Problem stellen die Gleitkommazahlen dar.

Allgemein kann man jede reelle Zahl x darstellen als

x = m * B^e

m steht für die Mantisse

B für die Basis

e für den Exponenten

Beispiel:   x = 12,353 = 1,2353 * 10¹ = 0,12353 * 10²

Wie man an dem Beispiel auch sieht, ist die Darstellung in dieser Form unterschiedlich möglich. Es gibt aber eine Norm, die besagt, dass vor dem Komma keine Null stehen soll. Diese Form nennt man deshalb auch Normalisierte Gleitkommazahl. Die normalisierte Form der Darstellung im obigen Beispiel ist also 1,2353 * 10¹.

Da wir hier im Dualsystem rechnen, haben wir bei der Darstellung der Zahlen also die Basis 2. Es müssen also nur die Mantisse und der Exponenten im Dualsystem dargestellt werden.

Darstellung im IEEE-Format

Das IEEE (sprich Ei triple I, Institute of Electrical and Electronics Engineers) hat für die Darstellung von Gleitkommazahlen Standards herausgegeben: IEEE-Standard 754-1985. Es gibt eine kurze (float) und eine lange Version (double)

Dieser besagt, dass in 32Bit (float) die Gleitkommazahl wie folgt abgelegt wird:

Das Vorzeichen benötigt ein Bit, der Exponent 8 Bits und die Mantisse 23 Bits.

Die im 32 Bit Modus größte darstellbare Zahl liegt knapp unter:

2¹²⁸10³⁸

^Die kleinste darstellbare positive Zahl lautet

2^{- 149} 10^{- 45} 

In der langen Darstellung in 64 Bit (double) benötigt das Vorzeichen 1 Bit, der Exponent 11 Bits und die Mantisse 52 Bits.

Damit erhält man natürlich andere darstellbare Größen:

Damit liegt die größte darstellbare positive Zahl knapp unter 10³⁰⁸

Die kleinste darstellbare positive Zahl lautet

2^{- 52} • 2^{- 1022} = 2^{- 1074} 10^{- 324}