© Prof. Dr. Knut
Barghorn, Jade Hochschule.
Studienort WHV. E-mail: knut.barghorn@jade-hs.de
Informatik 1, Kapitel 2: Boolesche Algebra
2. Boolesche Algebra
2.1 Lernziele, Literaturtipps und URLs
Ziel dieser
Einheit
Bislang sind wir in der Lage,
Informationen in Speichern korrekt abzulegen. Wir kennen die
Dualzahlen und wissen, wie die wesentlichen Informationen sich binär
(dual) darstellen lassen. Nun nähern wir uns langsam an die
interne Funktion eines Rechners an. Dabei interessiert nicht so sehr,
wie die elektronischen Vorgänge innerhalb eines Rechners
ablaufen, sondern vielmehr, wie die interne Logik funktioniert. Wir
schauen uns an, wie sich mit einfachen Grundfunktionen komplexe
Maschinen aufsetzen lassen. Dazu bedienen wir uns der der klassischen
Aussagenlogik. Wir werden die Boolesche Algebra mit den wesentlichen
Aussagen kennen lernen.
Literaturtipps
- Dieses Skript,
0,00 EUR , Für die Klausur ausreichend.
- Das Internet, "Google-Suche zu den einzelnen Themengebieten",
0,00 EUR , Es gibt zu dem Thema einige informative Seiten im Internet.
- Die Bibliothek, "Boolesche Algebra" oder "Logische Schaltungen" oder "Logik",
, Es gibt so viele gute Bücher, dass ich keines hervorheben möchte.
2.2 Booleschen Algebra – Erste Schritte
Wir
haben in Zahlensysteme festgestellt, dass die interne Logik von
Computern auf einem dualen Zahlensystem basiert. Die Informationen
können mit den Werten 0,1 abgelegt und vorgehalten werden.
Um
Manipulationen an den Informationen vornehmen zu können, bedarf
es Rechengesetzen, die eben auf dieser zweiwertigen Menge
funktionieren.
Glücklicherweise
existiert eine Logik, die genau für diesen Zweck entwickelt
wurde. Die von George Boole (1815 – 1864) 1847 veröffentlichte
Abhandlung mit dem Thema "An
Investigation of the Laws of Thought" widmet sich genau
dieser Problemstellung.
Die vorgestellte Algebra wird
mittlerweile nach George Boole auch als Boolesche Algebra bezeichnet.
Die Algebra hat vielfältige Anwendungsmöglichkeiten. So
können neben mengenalgebraischen Problemen auch Darstellungen
zur Aussagenlogik und die algebraische Beschreibung und Manipulation
von Schaltkreisen abgedeckt werden.
Drei wesentliche Gebiete sind auch für
die Informatik interessant:
- die Mengenalgebra,
- die Aussagenlogik,
- die Schaltalgebra.
Nebenbei
sei noch erwähnt, dass die Algebra von Boole im Laufe der Zeit
weiterentwickelt und ergänzt wurde. Besonderen Anteil daran
hatten John Venn und Charles Peirce
Wir werden im Verlauf dieses Abschnitts auch noch die Herren
Hamilton, de Morgan und Shannon kennen lernen. Letzterer ist für
die Entwicklung der so genannten Schaltalgebra verantwortlich
Anschauliche
Darstellung
Die
Boolesche Algebra operiert mit wahren (true) und unwahren (false)
Aussagen. Da es nur diese zwei Zustände gibt, können wir
diese auch als 1 und 0 darstellen.
In
der Booleschen Algebra behandelt man die Verknüpfung von binären
Aussagen (Wahrheitswerte) durch logische Operatoren, deren Ergebnisse
wieder Wahrheitswerte sind.
|
Verknüpfung
|
Name
|
Schreibweise
|
|
nicht a
|
Negation
|
¬a
|
|
a und b
|
Konjunktion
|
a ∧ b
|
|
a oder b
|
Disjunktion
|
a ∨ b
|
|
Wenn a dann b
|
Implikation
|
a ⇒ b
|
|
a genau dann wenn b
|
Äquivalenz
|
a ⇔ b
|
Wenn
wir zur Veranschaulichung die Mengenlehre hernehmen, können wir
einige Bilder zeichnen. Die Diagramme zu Darstellung heißen
Venn-Diagramme.
In Venn-Diagramm werden die Argumenten-Mengen und die Ergebnis-Menge
derart zusammengefasst, dass eine einfache Interpretation möglich
wird. Die
beiden Mengen werden durch unterschiedliche Merkmale charakterisiert:
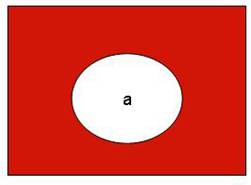
Die
Argumenten-Mengen werden durch einfache Einkreisungen gekennzeichnet,
wobei das entsprechende Argument innerhalb der (kreisförmigen)
Fläche den Wert "1" annehmen soll.
Die
Ergebnis-Menge wird über eine Farb- oder Schattierungsgebung
gekennzeichnet, wobei eine "1" z.B. durch eine dunklere
Farbe angegeben werden kann.
Die Negation
In
der Aussagenlogik ist diese Operation schnell begriffen:
Die
Aussage: „Wenn es morgen regnet, gehe ich nicht ins Freibad“
enthält eine Negation. Wenn die Aussage „wenn es morgen
regnet“ wahr ist, ist die Aussage „gehe ich ins Freibad“
nicht wahr.
Die
Wahrheitswertetabelle für die Negation (also den Operarator
¬
)
ist schnell aufgestellt:
Die Konjunktion
In
der Aussagenlogik lässt sich hierfür ebenfalls schnell ein
Beispiel finden:
„Wenn
morgen die Sonne scheint und es wärmer als 20 Grad Celsius ist,
gehe ich ins Freibad“
Hier
kommt die UND – Verknüpfung zum tragen. Die Aussage „gehe
ich ins Freibad“ ist nur dann wahr, wenn sowohl die Aussagen
„die Sonne scheint“ und „es ist wärmer als 20
Grad Celsius“ wahr sind. Beide Bedingungen müssen also
erfüllt sein.
Als
Venn-Diagramm dargestellt sieht die Konjunktion folgendermaßen
aus:
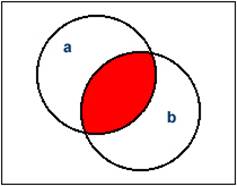
Alle
Werte, die gleichzeitig der Menge a und der Menge b angehören
sind wahr. Man spricht hier auch von der UND (AND) Verknüpfung.
Die
zugehörige Wahrheitstabelle ist schnell aufgestellt.
|
a
|
b
|
a ∧ b
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Wenn wir diese Wahrheitstabelle
etwas weiter fassen wollen und die Anzahl der zu verknüpfenden
Werte auf eine beliebige Anzahl erhöhen:
xN = x1 ∧ x2 ∧
x3 ∧ x4 ∧
….. ∧ xn,
dann
ist xN genau dann 0 wenn mindestens ein Element xi den Wert 0 hat.
Andersherum
kann die Aussage aber auch formuliert werden: xN ist genau dann 1,
wenn alle xi den Wert 1 annehmen.
Die Disjunktion
In
der Aussagenlogik findet sich auch hier schnell ein Beispiel:
„Wenn
es morgen schneit oder die Straßen glatt sind, werde ich mit
der Bahn zur Arbeit fahren“
Die
Aussage „mit der Bahn zur Arbeit fahren“ wird wahr, wenn
nur eine der Bedingungen „morgen schneit“ oder „Straßen
glatt“ wahr ist. Es müssen hier also nicht beide
Bedingungen zutreffen, sondern es reicht eine von beiden Bedingungen.
Als
Venn-Diagramm kann man die Disjunktion auch darstellen als
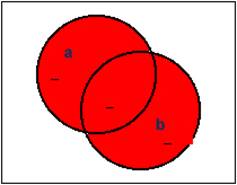
Damit
sind alle Werte, die der Menge a angehören genau Teil der Menge
a ∨ b
wie auch die Werte der Menge b. Der einzelne Wert gehört also
der Menge a oder b an. Deshalb spricht man auch von der ODER (OR)
–Verknüpfung.
Die Wahrheitstabelle auf die
binären Darstellungen für die Konjunktion sind also
|
a
|
b
|
a ∨ b
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
Wenn wir diese Wahrheitstabelle
etwas weiter fassen wollen und die Anzahl der zu verknüpfenden
Werte auf eine beliebige Anzahl erhöhen:
xN = x1 v x2 v x3 v x4 v …..v xn,
dann ist xN genau dann 1 wenn
mindestens ein Element xi den Wert 1 hat.
Die Implikation
Die Implikation wird häufig mit dem Satz "wenn a dann b" beschrieben.
In der Aussagenlogik findet sich hier ein Beispiel in dem Satz:"Wenn es regnet, werden die Bäume nass."
Dabei müssen wir jedoch etwas vorsichtig sein, es gilt also auf jeden Fall, dass die Bäume nass werden, wenn es regenet. Es kann aber auch andere Gründe für nasse Bäume geben (Sie werden vielleicht gesprengt).
Die zweite Aussage "Nasse Bäume" kann also wahr sein, ohne dass die erste Aussage "es regnet" wahr ist.
Es gilt aber immer, dass, wenn es regnet, die Bäume nass werden. Es kann nicht sein, dass die Bäume nicht nass werden.
Zur Veranschaulichung sehen wir uns die Wahrheitswertetabelle an:
|
a
|
b
|
a ⇒ b
|
|
0
|
0
|
1
|
|
0
|
1
|
1
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Die Implikation ist also eine Möglichkeit aus einer Aussage eine andere Aussage herzuleiten.
Deshalb bezeichnet man
a als Prämisse
und b als Conclusio
Es finden sich in der Literatur auch noch andere "Aussagen" für die Implikation.
- a impliziert b
- aus a folgt b
- wenn a gilt, dann gilt auch b
- a ist hinreichend für b
- b ist notwendig für a
Die Implikation läßt sich aus den bereits bekannten Opterationen ableiten.
(a ⇒ b) = (¬a ∨ b)
Die Äquivalenz
Hier hören wir schon, um was es gehen soll. Die Gleichheit wird überprüft.
Dann, wenn a und b gleich sind, wird das Ergebnis wahr.
|
a
|
b
|
a ⇔ b
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Aufgabe: Überprüfen Sie anhand von Wahrheitswertetabellen die Aussage: (a ⇒ b) ∧ (b ⇒ a) = (a ⇔ b). Führen Sie den "Beweis" über die Operatoren "∧, ∨ ¬.
Die Antivalenz / Kontravalenz
Wenn wir schon gerade dabei sind uns besondere Funktionen anzusehen, sollten wir die Antivalenz auch besprechen. Hier geht es eben darum, dass a und b nicht gleich sein sollen, um ein wahres Ergebnis zu erhalten.
Die Funktion wird immer dann wahr, wenn a und b unterschiedlich sind. Sie wird immer unwahr, wenn die Operanden gleich sind.
|
a
|
b
|
a ≠ b
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
0
|
Diese Funktion wird Ihnen in der Informatik ebenfalls immer wieder begegnen. Sie werden schon in einem der nächsten Kapitel eine Anwendug dieser Funktion erleben.
Man bezeichnet diese Funktion auch als die Boolesche XOR - Operation. XOR steht dabei für "Exklusives Oder". Sie merken, dass es sich wohl um eine "Oder"-Funktion handelt, aus der etwas ausgeschlossen wird.
Der Ausschluss liegt in der Situation a=1, b=1. Hier soll, anders als zur echten "Oder"-Funktion das Ergebnis nicht wahr werden.
So spricht man hier auch von "Entweder-Oder"-Funktion.
Die gebräuchlichen Zeichen dafür sind
Auch diese Funktion läßt sich zurückführen auf eine Funktion mit den Grundoperatoren.
a XOR b = (¬a ∧ b) ∨ (a ∧ ¬b)
Aufgabe: Welche Funktion ergibt sich aus der Verknüpfung (¬a ∧ ¬b) ∨ (a ∧ b) ?
2.3
Boolesche Algebra - Formalere Definition
Eine
Algebra wird durch Ihre Wertemenge, durch Ihre Operationen auf diese
Wertemenge und die dazugehörigen Rechengesetze bestimmt.
Bei
der Booleschen Algebra ist die Menge der Werte zweiwertig. Das heißt,
wir können die Wertemenge als 0,1 angeben.
Die
Operationen auf der Wertemenge sind ¬,
∧ , ∨ .
Begriffserklärungen: Eine
Operation setzt sich zusammen aus dem Operator, der angibt, welche
Operation ausgeführt wird und dem Operanden, auf den sich die
Operation bezieht.
Die
einfachste Operation ist also eine Operation auf einem Operanden mit
einem einstelligen Operator, z.B. ¬ a.
Man spricht hier auch von einer unitären Operation.
Es
geht natürlich auch komplizierter: Eine Operation a
∧ b entspricht
einer binären Operation.
2.4
Rechenregeln für Boolesche Algebra
Die Boolsche Algebra ist
mathematisch eine Menge. Daraus folgt, dass es einige Theoreme gibt:
Null-Gesetze:
a ∧ 0 =0
Dahinter steckt nichts anderes, als
die Aussage, dass egal welchen Wert a annimmt, die AND-Verknüpfung
mit einer unwahren Aussage „0“ immer ein unwahres
Ergebnis erzeugt.
a ∨ 0 =a
Die OR-Verknüpfung von einem
Wert a mit einer unwahren Aussage „0“ nimmt immer das
Ergebnis a an.
Eins-Gesetze:
a ∧ 1 = a
Sie sehen, dass die AND-Verknüpfung
zwischen a und einem wahren Ergebnis „1“ immer den Wert a
annimmt, egal welchen Wert a hat.
a ∨ 1 = 1
Die OR-Verknüpfung von einem
Wert a mit dem wahren Ergebnis „1“ nimmt immer den Wert
„1“ (wahr) an.
Doppelte Negierung
¬ ( ¬ a)
= a
Wenn ich in der Ungangsprache die
doppelte Verneinung benutze, lande ich ebenfalls bei der Aussage
„ja“. Die zweifache Anwendung eines NOT-Operators auf
einen Operanden hebt sich auf.
Beispiel: „Das ist nicht
unwahr“ ist eine Aussage mit doppelter Verneinung. Die
äquivalente Aussage ist: „Das ist wahr“.
Idempotenzgesetze oder auch Identitätsgesetze:
a ∧ a = a
a ∨ a = a
Wenn ich zwei gleiche Werte
miteinander Verknüpfe (durch AND oder OR) erhalte ich den Wert
als Ergebnis.
Beispiel aus der Aussagelogik:
„Gestern schien die Sonne und
gestern schien die Sonne“ ist gleichbedeutend mit der Aussage
„Gestern schien die Sonne“
„Gestern schien die Sonne
oder gestern schien die Sonne“ ist gleichbedeutend mit der
Aussage „Gestern schien die Sonne“
Komplementgesetze:
a ∧ ( ¬ a)
= 0
Hier sehen Sie schnell, dass das
Gesetzt sinnvoll ist.
a ∨ ( ¬ a)
= 1
Schauen Sie wieder in die
Wahrheitstabellen oben und Sie werden feststellen, dass auch dieses
Gesetzt korrekt ist.
Kommutativgesetze:
a ∨ b = b ∨
a
a ∧ b
= b ∧ a
Bei der Verknüpfung mit AND,
wie auch bei der Verknüpfung mit OR spielt die Reihenfolge der
Operanden keine Rolle.
Assoziativgesetze:
(a ∨
b) ∨ c =
a ∨ (b ∨
c)
(a ∧ b) ∧
c = a ∧ (b ∧
c)
Bei Verknüpfungen einer “Art”
(AND oder OR) spielt die Reihenfolge der Anwendung der Operanden
keine Rolle. Eine Klammerung ist also überflüssig.
Distributivgesetze:
a ∧ (b ∨
c ) = (a ∧
b) ∨ (a ∧
c)
Der Ausdruck a ∧
(b ∨ c)
ist genau dann wahr, wenn a wahr ist
und einer der beiden Operanden b oder c wahr sind. Der Ausdruck (a
∧ b) ∨
(a ∧ c) ist
genau dann wahr, wenn einer der Klammerausdrücke wahr ist.
Entweder muss (a ∧ b) wahr
sein, oder (a ∧ c). Einer
der Klammerausdrücke kann aber nur dann wahr werden, wenn a wahr
ist und entweder b oder c auch wahr sind.
a ∨ (b ∧
c) = (a ∨ b) ∧
(a ∨ c)
Aufgabe:Stellen Sie einen ähnlichen „Beweis“ für das
zweite Distributivgesetz auf. Hinweis: Überlegen Sie erst, wann
der Ausdruck vor dem Gleichheitszeichen unwahr wird.
Kürzungsregeln:
Nun wollen wir uns noch mit
Kürzungsregeln beschäftigen. Bei der Umstellung nach diesen
Regeln werden Sie möglicherweise immer die Möglichkeit
haben, die Formeln durch einfaches kürzen zu vereinfachen.
1)
a ∨
(a ∧ b) = a
2)
a ∧
(a ∨ b) =
a
3)
a ∨
( ¬ a ∧
b) = a ∨
b
Beweis: a ∨ ( ¬ a
∧ b) lässt
sich nach dem Distributivgesetz schreiben als :
(a ∨ ¬ a)
∧ (a ∨
b). Nach dem Komplementgesetz ist
(a ∨ ¬ a)
= 1
1 ∧ (a ∨
b) = (a ∨ b) nach
dem Einsgesetz. q e d!
4)
a ∧
( ¬ a ∨
b) = a ∧
b
Hier gehen wir im Prinzip genauso
vor: a ∧ ( ¬ a
∨ b) = (a ∧
¬ a) ∨
(a ∧ b) = 0 ∨
(a ∧ b) = (a ∧
b)
5)
(a ∧
b) ∨ (a ∧
¬ b) = a
Beweis : (a ∧
b) ∨ (a ∧
¬ b) lässt
sich nach dem Distributivgesetz schreiben als:
a ∧ (b ∨
¬ b )
Nach dem Komplementgesetz
ist (b ∨
¬ b)
=1 also
a ∧ 1 nach
dem Eins-Gesetz ist a ∧ 1
=a. Was zu beweisen war.
6)
(a ∨
b) ∧ (a ∨
¬ b) = a
Beweis:
(a ∨ b) ∧
(a ∨ ¬ b)
lässt sich auch schreiben als
a ∨ (b ∧
¬ b). (Distributivgesetz)
a ∨ (b ∧
¬ b) ist
nach Anwendung des Komplementgesetzes a ∨
0. Diese ist aber nach dem Null-Gesetz
a ∨ 0 =a
Hausaufgabe: Zeigen Sie
unter Anwendung der Gesetze, dass die Kürzungsregeln 1+2 richtig
sind. Kleiner Trick: Manchmal muss man erst etwas erweitern, damit
alles gut wird.
de Morgan Gesetze:
Augustus de Morgan lebte 1806-1871
als englischer Mathematiker und ein Freund von Charles Babbage. Er
zeigte, dass jede Konjunktion durch eine Disjunktion (und umgekehrt)
ersetzt werden kann. Er erweiterte damit die von Boole aufgestellte
Logik um eine entscheidende Erkenntnis .
¬ (a ∧
b) = ( ¬ a ∨
¬ b)
¬ (a ∨
b) = ( ¬ a ∧
¬ b)
Shannonsches Gesetz:
Claude Shannon (1916-2001)
verallgemeinerte diese Regel von de Morgan und zeigte, dass die
Inversion eines jeden Ausdrucks, sofern er nur mittels der Operatoren
∧ , ∨
und ¬ (d.h.
Konjunktion, Disjunktion und Negation) gebildet wurde, erreicht
werden, indem man ∧ und
∨ vertauscht
und jedes Literal negiert.
Das klingt ziemlich kompliziert,
die Aussage kann aber auch ausgedrückt werden als:
Der invertierte Wert einer
Booleschen Funktion ist gleich dem Wert, den diese Funktion liefert,
wenn alle Operanden und Operatoren invertiert werden.
Beispiel: ¬ (a ∧ b ∨
c ∧ ¬ d)
= ( ¬ a ∨
¬ b ∧
¬ c ∨
d)
Aufgabe
zum Mitdenken: Bitte
rechnen Sie das mal ein einem einfachen Beispiel nach: >
(¬a ∧ ¬b) = ¬(a ∨
b) , indem
Sie die Wahrheitstabellen für diese Aussagen aufstellen.
Nun haben wir die einzelnen Gesetze
kennen gelernt und können damit umgehen. Zur besseren Übersicht
hier noch einmal die Gesetze zusammengefasst in einer Tabelle.
|
Name
|
Regel 1
|
Regel 2
|
|
Null Gesetz
|
a ∧ 0 =0
|
a ∨ 0 = a
|
|
Eins Gesetz
|
a ∧ 1 = a
|
a ∨ 1 = 1
|
|
Doppelte Negation
|
¬(¬a) = a
|
|
|
Idempotenzgesetz
|
a ∧ a = a
|
a ∨ a = a
|
|
Komplementgesetz
|
a ∧ (¬a) = 0
|
a ∨ (¬a) = 1
|
|
Kommutativgesetz
|
a ∧ b = b ∧
a
|
a ∨ b = b ∨
a
|
|
Assoziativgesetz
|
(a ∧ b) ∧
c = a ∧ (b ∧
c)
|
(a ∨ b) ∨
c = a ∨ (b ∨
c)
|
|
Distributivgesetz
|
a ∧ (b ∨
c) = (a ∧ b) ∨
(a ∧ c)
|
a ∨ (b ∧
c) = (a ∨ b) ∧
(a ∨ c)
|
|
Kürzungsregeln
|
a ∧ (a ∨
b) = a
a ∧ (¬a ∨
b) = a ∧ b
(a ∧ b) ∨
(a ∧ ¬b) = a
|
a ∨ (a ∧
b) = a
a ∨ (¬a ∧
b) = a ∨ b
(a ∨
b) ∧ (a ∨
¬b) = a
|
|
De Morgan Gesetze
|
¬ (a ∧ b) = (¬a ∨
¬b)
|
¬ (a ∨ b) = (¬a ∧
¬b)
|
|
Inversionsgesetz von Shannon
|
Ohne Beispiel
|
Ohne Beispiel
|
- Sie kennen Venn- Diagramme
- Sie kennen die Verknüpfungen
AND, OR, NOT sowie die Funktionen Implikation, Äquivalenz und Antivalenz.
- Sie können Wahrheittabellen zu
den Verknüpfungen aufstellen
- Sie wissen, dass es die obigen
Rechenregeln gibt und können diese anwenden.
2.5
Schaltalgebra
Nun haben wir begriffen, dass es in
der Booleschen Algebra die Verknüpfungen UND,OR,NOT gibt. Wir
kennen auch die Wahrheitswertetabelle dieser Verknüpfungen.
Wenn wir eine Wahrheitswertetabelle
aufstellen, die alle verschiedenen Wahrheitswertekombinationen
enthält, werden wir feststellen, dass es 16 Möglichkeiten
gibt.
|
a
|
b
|
F1
|
F2
|
F3
|
F4
|
F5
|
F6
|
F7
|
F8
|
F9
|
F10
|
F11
|
F12
|
F13
|
F14
|
F15
|
F16
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
Wenn wir nun sagen, die
Verknüpfungen seien jeweils eine Funktion, dann haben wir 16
verschiedene Funktionen. Die Funktionen haben natürlich alle
einen Namen, den ich Ihnen hier mit auf den Weg geben möchte.
|
Funktion
|
Name
|
Schreibweise
|
|
F1
|
Nullfunktion
|
0
|
|
F2
|
UND (AND)
|
a ∧ b
|
|
F3
|
Negation der Implikation
|
¬ (a ⇒ b)
|
|
F4
|
Identität a
|
a
|
|
F5
|
Negation der Implikation
|
¬ (b ⇒ a)
|
|
F6
|
Identität b
|
B
|
|
F7
|
Exklusives ODER (XOR)
|
(a ⊕ b) (oder auch (a xor b) )
|
|
F8
|
ODER (OR)
|
a ∨ b
|
|
F9
|
NICHT ODER (NOR)
|
¬ (a ∨ b)
|
|
F10
|
Äquivalenz (NXOR)
|
a ⇔ b
|
|
F11
|
Negation von b
|
¬b
|
|
F12
|
Implikation
|
b ⇒ a
|
|
F13
|
Negation von a
|
¬a
|
|
F14
|
Implikation
|
a ⇒ b
|
|
F15
|
NICHT UND (NAND)
|
¬ (a ∧ b)
|
|
F16
|
Einsfunktion
|
1
|
Um einige der Funktionen werden wir
uns nun ganz speziell kümmern, da sie für Schaltungen immer
wieder benötigt werden und Ihnen daher sicherlich mal wieder
über den Weg laufen werden.
Schaltsymbole
Nun haben
wir begriffen, dass es in der Booleschen Algebra verschiedene
Operationen gibt. Diese lassen sich natürlich auch durch
Schalter darstellen. Hier seien nun die wichtigsten Funktionen
dargestellt abgebildet.
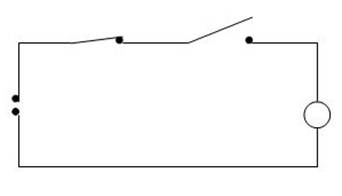
AND – Funktion
Wenn Sie beispielsweise eine AND –
Funktion in einer Schaltung darstellen wollen, können Sie dieses
sich am Besten durch einen Stromfluss klarmachen:
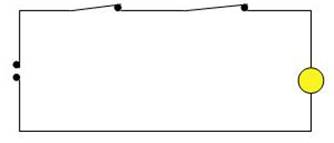
Die Lampe soll genau dann leuchten
(das Ergebnis true (1) sein), wenn beide Schalter den Wert true
annehmen (also beide Schalter geschlossen sind. Dazu werden die
beiden Schalter hintereinander (in Reihe) geschaltet.
Wenn einer der Schalter geöffnet
(„false) ist, leuchtet die Lampe nicht. Das Ergebnis wird
„false“.
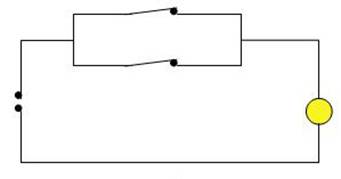
OR-Funktion
Bei einer OR-Funktion werden die
Schalter nicht in Reihe, sondern parallel geschaltet. Dadurch wird
erreicht, dass die Wahrheitswertetabelle der OR-Funktion bei den
verschiedenen Schalterstellungen stimmt.
Bei beiden geschlossenen Schaltern
leuchtet die Lampe, das Ergebnis wird „true“.
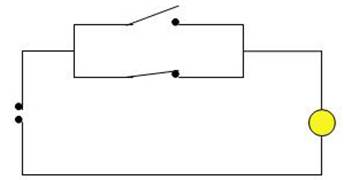
Aber auch bei einem geöffneten
Schalter bleibt der Stromkreis geschlossen. Das Ergebnis ist
ebenfalls wieder „true“.
NOT-Funktion
Die Negation
einer Aussage wird in der Schaltalgebra durch die Änderung der
Schalterstellung umgesetzt, ein geschlossener Schalter wird ein
geöffneter, ein offener Schalter wird geschlossen.
Da sich jeder
komplexe logische Ausdruck auf die elementaren Verknüpfungen
elementarer Ausdrücke zurückführen lässt, kann
dementsprechend auch jeder noch so komplexe logische Ausdruck durch
eine entsprechende Schaltung realisiert werden. Da komplexere
Schaltungen in dieser Darstellungsart sehr unübersichtlich
werden würden, hat man für die verschiedenen Booleschen
Funktionen Schaltsymbole eingeführt.
Übersicht über die Schaltsymbole
Leider unterscheiden sich die
Schaltsymbole in der europäischen und amerikanische Darstellung
etwas. In der Übersicht sehen Sie die Darstellung nach DIN
(nach 1976, davor sahen auch hierzulande die Symbole etwas anders
aus) und der Darstellung nach IEEE.
Diese Symbole nennt man logische
Gatter.
|
|
DIN 40900
|
IEEE
|
|
NOT
|

|
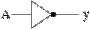
|
|
AND
|

|

|
|
OR
|
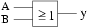
|
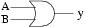
|
|
XOR
|

|
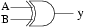
|
|
NAND
|

|

|
|
NOR
|
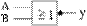
|
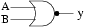
|
|
NXOR
|

|
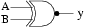
|
Nun wollen wir ein Beispiel für
eine Schaltung mit den neuen Schaltsymbolen darstellen.
Danach werden wir versuchen, die
Darstellung zu vereinfachen. Dazu werden wir wieder die Gesetze, die
wir bereits kennen gelernt haben, heranziehen.
Erste
Schaltungen
Nehmen wir uns ein erstes Beispiel
einer Realisierung einer Booleschen Verknüpfung vor:
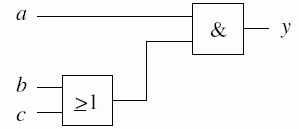
Gegeben sei die Verknüpfung
a ∧ (b ∨
c) = y
Dies können wir mit den
logischen Gattern in einem Schaltnetz darstellen.
Beispiel:
Wir haben den Ausdruck (a ∧
b) ∨ (a ∧
c) der sich als Schaltung darstellen
würde als
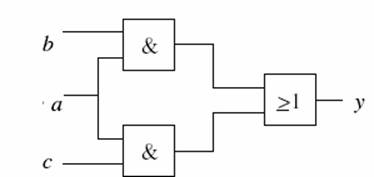
Nach Anwendung des
Distributivgesetzes: (a ∧ b)
∨ (a ∧
c) = a ∧ (b ∨
c) kann die Schaltung
auch dargestellt werden als
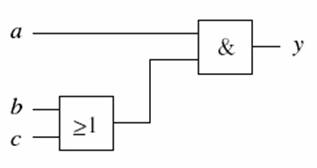
Der Vorteil ist klar
ersichtlich: Es werden nicht mehr drei, sondern nur noch zwei Gatter
benötigt.
Wie kommt man nun auf
die Zeichnung? In der Praxis geht man folgendermaßen vor:
- Zuerst wird die gewünschte Wahrheitswertetabelle aufgestellt.
- Dann sehen wir in der Tabelle der möglichen Booleschen
Funktionen nach, welche Funktion dem gewünschten Ergebnis
entspricht. Bei der Verknüpfung von mehreren Variablen (a,b,c,d
…) nutzen wir das Wissen, dass wir die Schaltfunktion aus der
Wahrheitswertetabelle konstruieren können (Boolesche Normalform)
- Danach formen wir die Schaltfunktionen so um, dass sie möglichst
einfach darstellbar und realisierbar ist.
Wenn Sie jetzt
aufgepasst haben, werden Sie merken, dass uns die Boolesche
Normalform noch gar nicht bekannt ist. Deshalb folgt nun ein kleiner
Einschub.
Boolesche
Normalformen
Mit Hilfe des Theorems der Booleschen
Normalform kann man aus einer Wahrheitswertetabelle einer Booleschen
Funktion einen Booleschen Ausdruck konstruieren. Die Schaltfunktion
wird dabei ausschließlich durch die drei Verknüpfungen
AND, OR, NOT ausgedrückt.
Disjunktive Normalform (DNF)
Das Entstehen einer disjunktiven
Normalform erläutert man ideal an einem Beispiel.
Wir nehmen eine Wahrheitswertetabelle
mit einer Verknüpfung von drei Operanden:
|
a
|
b
|
c
|
f(a,b,c)
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
Gesucht wird nun ein Boolescher
Ausdruck, der genau dieser Wahrheitswertetabelle entspricht.
Dazu bedient man sich der
Gesetzmäßigkeit der Bildung von disjunktiven Normalformen.
Die Bildung der disjunktiven Normalform funktioniert wie folgt.
Ich nehme jede Zeile mit dem Eintrag 1
in der Ergebnistabelle und bilde eine Konjunktion, die alle Variablen
der Funktion verknüpft. Variablen, die in der Zeile mit 1 belegt
sind, werden dabei nicht negiert und Variablen, die mit 0 belegt
sind, werden negiert.
Das hört sich sehr kompliziert
ist, ist es aber gar nicht:
Die Zeilen 2, 5 und 8 enthalten bei
Ergebnis eine 1.
Jetzt verknüpfe ich die Variablen
a,b,c durch eine Konjunktion. Dabei negiere ich die Variablen, bei
denen in der entsprechenden Zeile eine 0 steht.
Beispiel für Zeile 2 : ( ¬ a
∧ ¬ b
∧ c). Die
so gebildeten Terme werden Minterme genannt.
Das mache ich für jede Zeile mit
einer 1 in der Ergebnisspalte. Die einzelnen Zeilenergebnisse
verknüpfe ich danach durch eine Disjunktion
( ¬ a ∧
¬ b ∧
c) ∨ (a ∧
¬ b ∧
¬ c) ∨
(a ∧ b ∧
c) = f(a,b,c).
Damit die die erforderlich Schaltung
für das obige Problem bereits aufgestellt.
Konjunktive Normalform (KNF)
Auch die Bildung der konjunktiven
Normalform führt zum Ziel.
Die KNF wird sehr ähnlich
gebildet. Hier werden die Zeilen mit dem Eintrag 1 in der
Ergebnisspalte ignoriert. Es werden dafür die Zeilen mit dem
Eintrag 0 in der Resultatspalte herangezogen. Die Variablen mit einem
Eintrag 0 werden nicht negiert, die Variablen mit einem Eintrag 1 werden
negiert. Die nach dieser Methode gebildeten Terme heißen Maxterme.
|
a
|
b
|
c
|
f(a,b,c)
|
Maxterme
|
|
0
|
0
|
0
|
0
|
a ∨ b ∨ c
|
|
0
|
0
|
1
|
1
|
|
|
0
|
1
|
0
|
0
|
a ∨ ¬ b ∨ c
|
|
0
|
1
|
1
|
0
|
a ∨ ¬ b ∨ ¬ c
|
|
1
|
0
|
0
|
1
|
|
|
1
|
0
|
1
|
0
|
¬ a ∨ b ∨ ¬ c
|
|
1
|
1
|
0
|
0
|
¬ a ∨ ¬ b ∨ c
|
|
1
|
1
|
1
|
1
|
|
Die Maxterme werden nun über Konjunktionen verbunden:
( a ∨ b ∨ c)
∧ ( a ∨ ¬ b ∨ c)
∧ ( a ∨ ¬ b ∨ ¬ c)
∧ (¬ a ∨ b ∨ ¬ c)
∧ (¬ a ∨ ¬ b ∨ c)
Für die Bildung solcher
Normalformen gibt es auch systematisierte Verfahren (z.B. Karnaugh
Veitch Diagramme). Auf diese wollen gleich kurz eingehen eingehen.
Um nun zu einer Schaltung zu kommen,
sollten Sie den erhaltenen Booleschen Ausdruck aber noch etwas
vereinfachen.
Das können Sie gerne zu Hause
einmal machen, um Übung in der Umformung solcher Terme zu
bekommen.
Karnaugh-Veitch-Diagramme
Wenn wir einen Ausdruck vorliegen haben, ist manchmal sehr schwer zu sehen, ob dieser noch vereinfacht werden kann.
Das K-V-Diagramm bietet hier eine übersichtliche und schnelle Hilfe.
Die Vorgehensweise nach Karnaugh und Veitch ist grafisch orientiert und bietet einem eigentlich nur mehr Übersicht, als es die vielen Terme nach der Ermittlung von Normalformen es tun.
Allerdings muss man sagen, dass die K-V-Diagramme bei mehr als 4 Variabeln auch nicht mehr übersichtlich sind und daher dort kaum verwendet werden. Da gibt es dann wieder andere Verfahren, auf die wir hier nicht eingehen werden.
Man könnte nun eine Menge Mathematik betreiben zu zeigen, warum die K-V-Diagramme so gut funktionieren. Wir wollen und das ersparen und eher die Verwendung der K-V-Diagramme erlernen.
Nur soviel sei gesagt:"Dadurch, dass benachbarte Felder sich immer nur in einer Stelle unterscheiden, funktioniert es überhaupt".
Noch einen weiteren Satz: "Für die Verwendung benötigt man die disjunktive Normalform".
Gut klarmachen kann man sich die Anwendung eines Vorgangs immer genau dann, wenn man den Vorgang anwendet..... Es folgt also ein Beispiel:
Wir nehmen eine Lampe an, die bei folgender Schaltung leuchtet:
| C |
B |
A |
Lampe |
| 0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
1 |
Die disjunktive Normalform ist dazu schnell aufgestellt:
( ¬ a ∧
¬ b ∧
¬ c) ∨
( ¬ a ∧
b ∧
¬ c) ∨
(a ∧
b ∧
¬ c) ∨
( ¬ a ∧
¬ b ∧
c) ∨
( ¬ a ∧
b ∧
c) ∨
(a ∧
b ∧
c)
= f(a,b,c).
Diese Funktion ist noch etwas unbequem gross. Wir wollen sie nun vereinfachen. Entweder rechnen Sie nun mit Hilfe der Rechengesetze der Booleschen Algebra, oder sie benutzen ein K-V-Diagramm.
Wir entscheiden uns für das K-V-Diagramm.
Wir nehmen nun einfach die Minterme her und setzen in eine vorbereitete Matrix an den richtigen Stellen eine 1.
| |
a |
a |
¬a |
¬a |
| b |
1 |
1 |
1 |
1 |
| ¬b |
0 |
0 |
1 |
1 |
| |
c |
¬c |
¬c |
c |
Wie man nun sehr deutlich sieht, stehen einige Einsen in Reihe nebeneinander oder untereinander.
Blöcke von 2, 4, 8 oder allgemein kn Einsen lassen sich zusammenfassen. n ist die Anzahl der Variablen.
Hier lassen sich also zwei Blöcke bilden. Die Einsen in der Zeile mit dem b
Der Block von 4 Einsen bei ¬a.
Die obige Funktion kann also mit ¬a ∨ b recht schnell ausgedückt werden.
Die haben sich das komplizierte Umstellen und Rechnen erspart.
Sie sollten aber bitte zu Hause einmal nachrechnen, ob ich auch alles richtig gemacht habe.
Um gleich zu sehen, ob Sie es verstanden haben, folgt ein weiteres Beispiel. Diesmal werden wir vier Variabeln einfliessen lassen.
Nehmen wir an, wir haben folgendes K-V-Diagramm ausgefüllt vorliegen:
| |
a |
a |
¬a |
¬a |
|
| b |
0 |
0 |
0 |
0 |
¬d |
| b |
1 |
0 |
0 |
0 |
d |
| ¬b |
1 |
1 |
1 |
1 |
d |
| ¬b |
0 |
0 |
0 |
0 |
¬d |
| |
c |
¬c |
¬c |
c |
|
Hier haben wir einen Block von Einsen in der Reihe ¬b und d. Damit ist ein Term bestimmt.
Einen anderen Block haben wir bei a und c und d vorliegen. Damit läßt sich unsere gesuchte Funktion ausdrücken als:
( ¬ b ∧
d) ∨ (a ∧ c ∧ d) = f (a,b,c,d)
Sie sehen, das Vorgehen ist recht schnell und einfach. Sie müssen lediglich beachten, dass Sie die richtigen Diagramme zur Hand haben.
Es fehlt Ihnen nun noch das Diagramm für zwei Variabeln. Hier ist es:
2.6
Anwendungen (Addierer)
Halbaddierer
Wir haben bereits gesehen, dass die
Grundrechenarten in Dualen Zahlensystem sich alle auf das Addieren
zurückführen lassen. Nun wollen wir uns ansehen, wie ein
Rechner eigentlich intern rechnet. Wir bauen dazu ein Schaltbild für
einen Addierer auf.
Zunächst stellen wir die
Wahrheitswertetabelle für das Addieren auf. Bei Addieren müssen
wir aber berücksichtigen, dass wir Überträge (das so
genannte Carry-Bit) haben. Wir haben also zwei Wahrheitswertetabellen
zu berücksichtigen.
|
a
|
b
|
F(a,b)
|
Carry
|
|
0
|
0
|
0
|
0
|
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
0
|
|
1
|
1
|
0
|
1
|
Aus der Tabelle der möglichen Funktionen
unter Kapitel 2.5 erkennen wir sehr schnell, dass wir die
Funktion F7 (XOR) für das Resultat benötigen. Den Übertrag
decken wir über die Funktion AND ab.
Damit ist die Schaltfunktion eines Halbaddierer
bereits fertig:
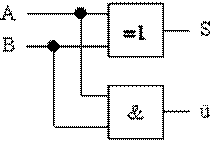
Volladdierer
Wenn ich aber richtig addieren möchte,
muss ich den Übertrag des vorangegangenen Schrittes mitnehmen
und als weiteren Eingangswert spezifizieren.
Die Schaltfunktion wird dadurch aber nur
unwesentlich komplizierter.
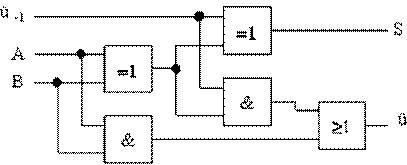
Wir erinnern uns, dass wir die Subtraktion auf
eine Addition mit dem Zweierkomplement zurückführen können.
Damit ist dieses Problem also auch schon gelöst.
Die Multiplikation und Division lassen sich
zwar auch auf die Addition zurückführen, aber dazu braucht
es noch eine weitere Einheit, nämlich so genannte
Schieberegister, auf die wir hier aber nicht weiter eingehen wollen
- Sie kennen die Booleschen Funktionen. Dabei wissen Sie genau, wie die Funktionen AND, NOT, OR, NAND, XOR gebildet werden.
- Sie kennen die Schaltsymbole nach DIN 40900;
- Sie können einfache Schaltungen lesen und in eine Boolesche Funktion übertragen
- Sie können aus einer Wahrheitswertetabelle anhand der Normalformen eine Boolesche Funktion ableiten
- Sie kennen die Karnaugh-Veitch-Diagramme und können diese anwenden











