© Prof. Dr. Knut Barghorn, Jade Hochschule. Studienort WHV. E-mail: knut.barghorn@jade-hs.de
Das Ziel dieses Abschnitts ist, Sie mit dem EVA-Prinzip vertraut zu machen. Im vorhergehenden Abschnitt haben wir dieses Prinzip bereits kennen gelernt. Die Hardware arbeitet genau nach diesem Prinzip. Wir werden dieses Prinzip an anschaulichen Darstellungen aus dem alltäglichen Leben einüben.
Sie werden Begriffe wie Algorithmen, Prozesse und Turing Maschine kennen lernen. Auch hier werden wir die Begriffe auf anschauliche Art und Weise begreifen lernen. Dabei werden wir aber auch die formalen Beschreibungen von Algorithmen durch Diagramme kennen lernen.
Danach werden wir uns auf die Begriffe Ein- und Mehrprozessorsysteme, Parallelverarbeitung und Multitasking stürzen, womit dieser Abschnitt dann auch schon endet.
Wenn Sie bei Google nach dem EVA-Prinzip suchen, werden Sie feststellen, dass das EVA-Prinzip nicht auf die Informatik beschränkt ist.
Der Dozent spricht einen Studenten an, der seiner Meinung nach vor sich hin döst. Er stellt ihm die Frage, welches Kapitel gerade behandelt wird. Der Student schaut auf die Tafel und sieht die Überschrift des Kapitels. Er antwortet geistesgegenwärtig: "Das EVA-Prinzip".
Damit hat er als Prozessor innerhalb eines EVA-Prinzips gehandelt.
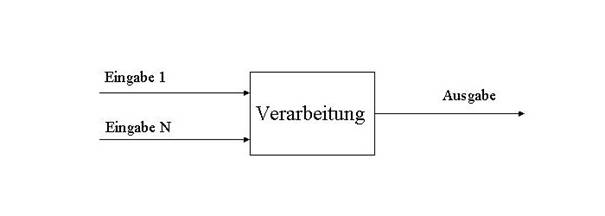
Eingabe: Frage des Dozenten, Tafelbild
Verarbeitung: Lesen der Überschrift
Ausgabe: Beantwortung der Frage
Eine andere Situation wäre, der Student geht in die Mensa und möchte etwas essen. Er steht am Aushang und liest, dass es heute zwei Gerichte (Gericht 1: Gebratene Leber, Gericht 2: Erbseneintopf)gibt. Er entscheidet sich für die Erbsensuppe, da er Leber nicht ausstehen kann. An der Ausgabe angekommen bestellt er die Erbsensuppe.
Aufgabe: Bitte geben Sie die Eingabe, die Verarbeitung und die Ausgabe an.
Wie kann ein solcher Prozess übersichtlich dargestellt werden? Es gibt in der Informatik dafür natürlich formalisierte Diagramme.
Eines dieser Diagramme ist das SADT-Diagramm. (SADT steht für Structured Analysis and Design Technique)

Aufgabe: Wie sähe ein SADT - Diagramm für die obige Aufgabe aus? Bitte zeichnen Sie es auf.
Nehmen wir ein drittes Beispiel: Wir sind zwar hier nicht im Kurs „Backen für Anfänger“, aber an einem Rezept für Apfelkuchen kann die Abarbeitung eines Prozesses sehr anschaulich dargestellt werden.
Hier also das Rezept:
4 Eier
350 g Zucker
120 g Butter
1/8 l Milch
300 g Mehl
7 säuerliche Äpfel
3 TL Backpulver
1 EL Zimt
3 EL Zucker
Die Eier aufschlagen und das Eiweiß und Eigelb in eine Schüssel geben. Den Zucker dazugeben und die Masse schaumig rühren. Butter und Milch dazugeben und die Masse aufkochen. Zum Schluss das Mehl und das Backpulver unter die Masse ziehen. Den dünnen Teig auf ein Blech geben. Äpfel in Scheiben schneiden. Die Apfelscheiben auf dem Teig verteilen. Zimt und Zucker mischen und danach auf dem Teig verteilen. Bei 200 Grad C. eine halbe Stunde backen.
Das vereinfachte SADT-Diagramm sieht nun aus wie folgt:
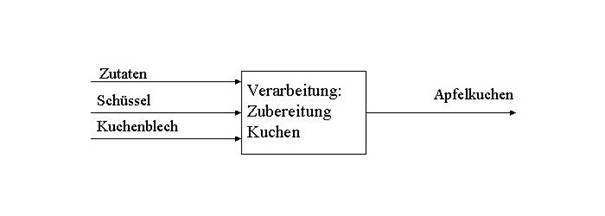
Die Verarbeitung stellt einen Prozess dar. Diesen Prozess müssen Sie durchführen um einen Apfelkuchen dieser Art zu erhalten.
Computer führen Prozesse auch sehr schnell aus und haben eine weitere positive Eigenart: Der Computer macht genau das, was man ihm sagt.
Der Prozess der Zubereitung des Kuchens ist im Rezept ebenfalls dargestellt. Bei einem Computer haben wir zwar andere Prozesse, aber das Vorgehen ist gleich. Wenn Sie genau hinsehen, habe ich hier exakt geschrieben, dass Sie nicht die Eier, sondern das Eiweiß und das Eigelb in die Schüssel geben (Das wird in einem normalen Rezept häufig nicht geschrieben). Hier würde sich die Eigenschaft des Computers, genau das Gesagte schnell zu erledigen, deutlich negativ auswirken.
Eine weitere Einschränkung bei Computern ist, dass er die Anweisungen auch verstehen muss. So sind z.B. die Abkürzungen im Rezept TL (Teelöffel) und EL (Esslöffel) möglicherweise nicht jedem geläufig und der Prozessor weiß nicht, was zu tun ist. Ein anderes Problem kann sein, dass die Anweisungen nicht ausgeführt werden können. In dem Rezept oben ist beispielsweise kein Messer erwähnt, mit dem die Äpfel geschnitten werden können. Damit ist der Schritt Äpfel zerteilen nicht ausführbar. Bei einem Computer sind solche fehlenden Informationen problematisch. Der Prozess „hängt“.
(Wer das EVA-Prinzip gerne zu Hause nachbereiten möchte ist herzlich dazu ausgefordert. Ihre Ausgabe können Sie zur nächsten Veranstaltung mitbringen. Ihre Kommilitonen werden gern beurteilen, ob Sie die Prozessverarbeitung verstanden haben.)
Die Beschreibung des Prozesses der Verarbeitung nennt man Algorithmus. Eigentlich beschreibt das Wort Algorithmus nur eine allgemeine Darstellung für einen Lösungsweg. (Wir haben bereits vorher gehört, dass das Wort vom Namen eines Arabers stammt.)
Beispiele aus dem täglichen Leben gibt es hinreichend viele:
|
Prozess |
Ausführender |
Algorithmus |
Beschreibung |
|
Kuchen backen |
Student |
Rezept |
Nimm 500 g Mehl |
|
Spielen einer Klaviersonate |
Pianist |
Partitur |
|
|
Bau eines Radios |
Bastler |
Bauanleitung
|
Verbinde Transistor 1 mit Transistor 5 |
|
Telefonieren |
Anrufer |
Bedienungsanleitung |
Drücken Sie die Sterntaste (*) |
In der Informatik sind Algorithmen zentraler Themenbestandteil:
· Algorithmentheorie
· Komplexitätstheorie
· Berechenbarkeitstheorie
· Computerprogramme
· Elektronische Schaltkreise des Computers
Was ist nun aber genau ein Algorithmus. Bislang haben wir zwar eine etwaige Vorstellung, aber keine Definition. Dies störte auch die Mathematiker des 19ten und 20ten Jahrhunderts. Die normale Sprache reicht auf Grund Ihrer Unschärfe und Widersprüchlichkeiten nicht aus, um eine eindeutige und widerspruchsfreie Definition zu erhalten. Deshalb bemühte man sich seit Anfang des 20ten Jahrhunderts mit verschiedenen Ansätzen um eine Definition.
Definition: Eine Berechnungsvorschrift zur Lösung eines Problems heißt Algorithmus genau dann, wenn eine für diese Berechnungsvorschrift äquivalente Turing-Maschine existiert, die für jede Eingabe stoppt.
Nun sind wir nicht viel schlauer als vorher, weil wir nun erst einmal klären müssen, was eine Turing-Maschine ist.
Die Turingmaschine ist ein von dem britischen Mathematiker Alan Turing 1936 entwickeltes mathematisches Konstrukt um eine Klasse von berechenbaren Funktionen zu bilden.
Was das genau bedeutet werden wir gleich verstehen. Zunächst schauen wir uns die Bestandteile der Turingmaschine an.
Eine Turing Maschine besteht aus
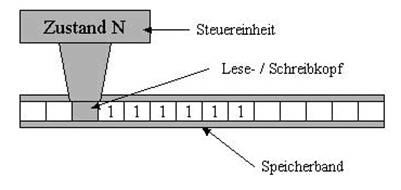
Abbildung Turing Maschine
Die Turing Maschine kann natürlich noch nicht ohne Programm arbeiten. Das Programm soll festlegen, wie die vorhandene Bandbeschriftung verarbeitet werden soll. Hier kommt also der Algorithmus zum tragen:
Beispiel eines Programms für die Turing Maschine :
(z1,1) -> (z2,1,R)
(z1,_) -> (z1,_,R)
(z2,1) -> (z2,1,R)
(z2,_) -> (z2,1,H)
Wenn wir das Programm nun durchlaufen, sehen wir, wie die Maschine arbeitet.
Zunächst sind wir im Zustand 1 und finden ein Leerzeichen im Feld auf dem der Lese-/Schreibkopf steht. Laut Anweisung sollen wir dann im Zustand 1 bleiben und ein Leerzeichen auf das Feld schreiben. Dann soll der Lese-/Schreibkopf noch um einen Schritt nach Rechts bewegt werden.
Wir sind damit im Zustand 1 und finden eine1. Nun soll der Zustand auf 2 wechseln und eine 1 schreiben und nach Rechts laufen.
Danach sind wir im Zustand 2 und finden eine 1 auf dem Band. Wir sollen im Zustand 2 bleiben, eine 1 schreiben und nach Rechts gehen.
Wir sind noch mal im Zustand 2 und finden eine 1. Bleibe im Zustand 2, schreibe eine 1 und gehe nach Rechts.
Und noch mal wie vorher.
Wir sind im Zustand 2 finden ein Leerzeichen. Die Anweisung lautet: Bleibe im Zustand 2, schreibe eine 1 und Halt.
Damit ist das Programm vollständig durchlaufen. Man kann sich natürlich auch weitaus komplexere Programme überlegen. Ein Beispiel werden wir ebenfalls noch durchlaufen.
Das nächste Beispiel soll zeigen, dass man mit Turing Maschinen auch wirklich rechnen kann. Wir addieren dazu zwei Zahlen.
Die Mathematische Formel lautet: 3+2=
Die Bandbelegung ist damit wie folgt:
1 1 1 + 1 1 =
(drei Einsen (je Feld eine) gefolgt von einem Plus Zeichen gefolgt von zwei Einsen und gefolgt von einem Gleichheitszeichen.
Wie können wir sinnvoll vorgehen um nachher auf dem Band fünf Einser in Folge stehen zu haben?
Laufe nach rechts, solange bis das Plus Zeichen entdeckt wird.
Lösche das Plus Zeichen und schreibe eine Eins
Laufe weiter nach Rechts und finde das Gleichheitszeichen
Lösche das Gleichheitszeichen
Lösche die letzte Eins.
Das notwendige Programm dazu sieht folgendermaßen aus:
(z1,+) -> (z1,1,R)
(z1,1) -> (z1,1,R)
(z1,=) -> (z2,_,L)
(z2,1) -> (z2,_,H)
Aufgabe : Vollziehen Sie den Ablauf des Programms nach
Die Turing Maschine kann also addieren. Sie kann im Übrigen auch die anderen Grundrechenarten (subtrahieren, dividieren, multiplizieren).
Die Turing Maschine kann aber nicht nur rechnen, sondern auch z.B. sortieren.
Auch hierzu ein kleines Beispiel:
Eine Zeichenkette bestehen aus ungeordneten As und Bs soll geordnet werden:
A B A A B B B A B A
Die Strategie ist: Finde ein A, lösche es und laufe an das Ende der Bandbeschriftung und füge dort ein A ein. Das mache solange, bis kein A mehr zu finden ist.
Dann: Finde ein B, lösche es, laufe an das Ende der Bandbeschriftung und füge dort ein B ein. Das mache, solange, bis kein B mehr zu finden ist.
Achtung: Dabei entstehen „Löcher“ auf dem Band (Leerzeichen), die natürlich entsprechend berücksichtigt werden müssen.
Achtung: Wir werden ein Problem bekommen, weil wir nicht wissen, ob nach den Löchern das Band bereits am Ende der Beschriftung angekommen ist. Wir bedienen uns also erst einmal eines kleinen Tricks. Wir markieren Anfang (mit einem §) und Ende (mit %) der Bandbeschriftung.
(z1,A) -> (z1,A,L)
(z1,B) -> (z1,B,L)
(z1,_) -> (z2,§,R)
Damit haben wir den Anfang markiert.
Aufgabe zum Mitarbeiten : Wie markiert man das Ende der Bandbeschriftung?
(z2,A) -> (z2,A,R)
(z2,B) -> (z2,B,R)
(z2,_) -> (z3,%,L)
So, die Maschine ist nun im Zustand 3 und wir müssen den Kopf erstmals nach vorne an den Anfang bringen. Das ist nun wieder recht einfach:
(z3,A) -> (z3,?,L)
(z3,?) -> (z3,?,L)
(z3,§) -> (z4,?,R)
Aufgabe zum Mitarbeiten : Was muss man statt der Fragezeichen einsetzen, damit es funktioniert?
(z3,A) -> (z3,A,L)
(z3,B) -> (z3,B,L)
(z3,§) -> (z4,§,R)
damit sind wir auf der ersten Position des Bandes angekommen und haben Zustand 4 erreicht. Nun kann das eigentliche Sortieren losgehen.
Wir suchen also nun das erste A auf dem Speicherband. Dazu überlegen wir, auf welche Feldinformation wir treffen können und überlegen, welche Aktion daraus folgt.
(z4,A) -> (z5,_,R)
Wir sehen ein A, wechseln den Zustand, weil wir nun eines erwischt haben, welche wir hinten einfügen wollen und gehen nach Rechts.
(z4,B) -> (z4,B,R)
Wir sehen ein B, lassen die Information und den Zustand unverändert und gehen nach Rechts
(z4,_) -> (z4,_,R)
Wir sehen eine Leerstelle. Auch hier gehen wir ohne Veränderung nach Rechts
(z4,%) -> (z7,%,L)
Wir erkennen das Ende der Eingabeinformation. Die Information lassen wir stehen, wechseln aber in einen neuen Zustand 7.
Wie Sie merken, haben wir nun zwei Möglichkeiten: Zustand 5 oder Zustand 7. betrachten wir zunächst den Zustand 5 (wir haben ein A gefunden und gelöscht)
Als nächstes müssen wir an das Ende der Bandbeschriftung laufen.
(z5,A) -> (z5,A,R)
(z5,B) -> (z5,B,R)
(z5,_) -> (z5,_,R)
(z5,%) -> (z6,%,R)
Wir erreichen unweigerlich das erste Feld nach der Endmarkierung.
Dort wollen wir das A in das erste freie Feld schreiben:
(z6,A) -> (z6,A,R) (Wir sehen ein belegtes Feld und gehen ohne Änderung nach Rechts)
(z6,_) -> (z?,A,L) (Wir sehen eine freie Position und schreiben das A dort hinein, gleichzeitig gehen wir nach Links)
Aufgabe zum Mitarbeiten : In welchen Zustand wechseln wir, damit wir weiter machen können? Hinweis: Wir sollten wieder vorne mit der Suche nach dem nächsten A beginnen.
Die Routine für das Rücklaufen auf die erste Position haben wir bereits geschrieben. Aber Vorsicht: wir haben, wenn Sie sich erinnern noch keine Möglichkeit für die plötzlich auftretenden Leerstellen entwickelt:
(z3,A) -> (z3,A,L)
(z3,B) -> (z3,B,L)
(z3,§) -> (z4,§,R)
Es sind nun auch folgende Feldinhalte möglich:
(z3,_) -> (z3,_,L) Wir lassen den Inhalt leer und gehen weiter nach Links
(z3,%) -> (z3,%,L) Wir lassen das Inhalt Endmarke stehen und gehen weiter nach Links
Diese Schleife (denn wir haben nichts anderes programmiert), lassen wir solange durchlaufen, bis wir kein A mehr in der Eingabe haben.
Aufgabe zum Mitarbeiten : Woran erkennen wir, dass kein A mehr da ist? Hinweis: Einen Zustand dafür haben wir schon definiert.
Nun kommt als nächstes die Sortierung der B. Dazu müssen Sie ausgehend vom Zustand 7 weiter machen. Aber das schaffen Sie jetzt allein in der Hausaufgabe
Aufgabe zum Mitarbeiten : Schreiben Sie das kleine Sortierprogramm allein weiter und senden Sie mir Ihr Programm per E-Mail. Hinweis. Den Zustand 3 können Sie nicht mehr verwenden. Zusatzfrage: Warum?
Sie haben nun die Turing Maschine kennen gelernt. Und Sie haben gesehen, wie sie arbeitet. Wenn wir auf unsere Definition eines Algorithmus zurückkommen, verstehen Sie diese.
Definition Algorithmus: Eine Berechnungsvorschrift zur Lösung eines Problems heißt Algorithmus genau dann, wenn eine für diese Berechnungsvorschrift äquivalente Turing-Maschine existiert, die für jede Eingabe stoppt.
Ich hatte Ihnen versprochen, dass wir uns noch einen mathematischen Algorithmus ansehen. Dazu nehmen wir den Algorithmus des Euklid.
Euklid suchte den größten gemeinsamen Teiler zweier natürlichen Zahlen A und B. Bei kleinen Zahlen können wir das selbstverständlich im Kopf. Nehmen wir die Zahlen 21 und 35. Der größte gemeinsame Teiler ist 7. Wer das kleine Einmaleins kennt, schafft das locker. Es gibt aber auch sehr große Zahlen z. B. 378 und 246, bei denen wir das im Kopf nicht hinbekommen.
Wenn wir die beiden Aufgaben einem Computer geben, ist es für ihn gleich schwer. Er kennt nämlich im Gegensatz zu uns das kleine Einmaleins nicht. Der Computer benötigt eine Berechnungsvorschrift. Eben diese hat Euklid um 300 v. Chr. entwickelt.
1) Sei A die Größere der beiden Zahlen A und B (entsprechend vertauschen, falls dies nicht bereits so ist)
2) Setze A = A – B
3) Wenn A und B ungleich sind, dann fahre fort mit Schritt 1, wenn sie gleich sind, dann beende den Algorithmus: Diese Zahl ist der größte gemeinsame Teiler.
Probieren wir es doch an den oben genannten Zahlen einmal aus.
|
|
A |
B |
A-B |
|
1. |
378 |
246 |
132 |
|
2. |
246 |
132 |
114 |
|
3. |
132 |
114 |
18 |
|
4. |
114 |
18 |
96 |
|
5. |
96 |
18 |
78 |
|
6. |
78 |
18 |
60 |
|
7. |
60 |
18 |
42 |
|
8. |
42 |
18 |
24 |
|
9. |
24 |
18 |
6 |
|
10. |
18 |
6 |
12 |
|
11. |
12 |
6 |
6 |
|
12 |
6 |
6 |
gleich |
Das Ergebnis ist also 6.
Aus der Definition von Algorithmen mit Hilfe der Turingmaschine können wir verschiedene Eigenschaften von Algorithmen ableiten. Dabei werden und wieder neue Begriffe begegnen, die es zu erläutern gilt.
Formale Definition:
Nach H. Kübe, der aus der oben stehenden Definition die Definition eines Algorithmus ableitete ist ein Algorithmus eine in der Beschreibung und Ausführung endliche, deterministische und effektive Vorschrift zur Lösung eines Problems, die effizient sein soll.
Diese Definition müssen wir Wort für Wort genauer betrachten:
Zum letzen Punkt kann man noch eine weitere Eigenschaft von Algorithmen anfügen, die unter dynamischer Finitheit bekannt ist: Die bei der Abarbeitung eines Algorithmus entstehenden Datenstrukturen und Zwischenergebnisse belegen nur endlich viel Speicherplatz.
Nun wollen wir uns noch ansehen, wie Algorithmen klassifiziert werden können. Ein Algorithmus heißt
Es folgen kleine Beispiele aus der Welt der der nichtdeterminierten, nichtterminierten, nichtdeterministischen Algorithmen:
Zunächst ein Beispiel für einen nichtdeterministischen Algorithmus.
Eingabe: Liste aller meiner Freunde Wiederhole für alle Freunde Führe willkürlich einen der folgenden Einzelschritte aus: Markiere Freund mit 1, den ich nächste Woche treffen soll Markiere Freund mit 2, den ich nächste Woche anrufen soll Lösche Freund aus der Liste Ende Willkür Ende Wiederhole Ausgabe: Liste aller Freunde mit Markierungen, ob ich sie treffen oder anrufen soll
Die Einzelschritte folgen nicht eindeutig. Es gibt hier eine nichtdeterministische Auswahl von verschiedenen Möglichkeiten.
Das Beispiel ist allerdings auch nichtdeterminiert. Die Ausgabe kann bei zwei Läufen durchaus verschieden sein.
Allerdings ist der obige Algorithmus terminierend. Nach der Abarbeitung der Liste stoppt der Algorithmus.
Anderes Beispiel:
Eingabe: Liste aller meiner Freunde Wiederhole, bis die Liste leer ist Wiederhole für jeden Freund Führe willkürlich einen der folgenden Einzelschritte durch Markieren Freund mit 1 Lösche Freund aus der Liste Ende Willkür Ende Wiederhole Ende Wiederhole Ausgabe: Bereinigte Freundesliste
Dieser Algorithmus ist nichtterminierend, da es nicht unwahrscheinlich ist, dass die willkürliche Auswahl “Lösche Freund“ nicht nach endlich vielen Schritten zur vollkommenen Löschung aller Einträge geführt hat. Allerdings ist der Algorithmus determiniert, da bei immer gleicher Eingabe auch das gleiche Endergebnis herauskommt. (Leere Liste)
In der Regel werden überall determinierte Algorithmen eingesetzt, da das Ergebnis sich bei gleicher Eingabe nicht unterscheiden soll.
Zur Durchführung von Berechnungen werden meist terminierende Algorithmen eingesetzt. Bei der Überwachung von Produktionsanlagen oder auch im Betriebssystem werden nichtterminierende Algorithmen eingesetzt.
Algorithmen, die an einer Stelle zwei oder mehr mögliche alternative Schritte aufweisen heißen nichtdeterministisch. Wenn man den Alternativen Wahrscheinlichkeiten zuordnen kann spricht man auch von stochastischen Algorithmen.
Aufgabe zum Mitdenken: : Ist ein terminierender, deterministischer Algorithmus grundsätzlich determiniert oder nichtdeterminiert?
Wir haben bei der Turing Maschine gesehen und auch in Euklidischen Algorithmus festgestellt, dass Teile der Bearbeitungsvorschrift öfter durchlaufen werden können.
Um den Ablauf einer Bearbeitungsvorschrift oder eines Algorithmus darzustellen, bedient man sich verschiedener Möglichkeiten:
Die Darstellung im Pseudocode erfolgt textuell und semiformal unanhängig von der später verwendeten Programmiersprache in so genannten Kontrollelementen und gibt die logische Abfolge des Ablaufs an.
Diese Kontrollelemente sind:
Eine Sequenz beschreibt die Abfolge der Anweisungen, die in vorgegebener Reihenfolge von oben nach unten abgearbeitet werden.
Beispiel:
Begin
Anweisungen
End
Eine Wiederholung ist ein Anweisungsteil, der auf Grund einer eindeutigen Bedingung eine bestimmte Anzahl von N-malen durchlaufen wird.
Beispiel:
WHILE.. DO ..
BEGIN
Anweisung
END
Die Auswahl stellt eine Verzweigung auf Grund einer eindeutigen Bedingung innerhalb des Programms dar. Je nach Bedingung wird der erste Teil oder der zweite Teil der Anweisung durchlaufen
Beispiel:
IF .. THEN ..
Anweisung
ELSE
Anweisung
END IF
Dieser Pseudocode ist erst einmal unabhängig von der Programmiersprache und deshalb
Die Nachteile sind aber:
Wenn Sie ein Programm schreiben wollen, ist es gerade bei komplexen Programmen notwendig, den Programmablauf in eine übersichtliche Struktur zu bringen.
Eine sehr weit verbreitete Darstellung ist der Programmablaufplan oder das Flussdiagramm oder einfach der Ablaufplan.
Diese Art der Visualisierung hilft gerade bei kleinen Problemstellungen oder Algorithmen
Die Elemente der PAPs sind recht einfach:
|
Name |
Darstellung |
Beschreibung |
|
Grenzstelle |
|
Kennzeichnet Anfang und Ende des Programms / Ablaufplans |
|
Marke |
|
Verzweigungspunkte (mehrere Eingänge aber nur einen Ausgang |
|
Ein-/Ausgabeanweisung |
|
Ein Eingang, ein Ausgang |
|
Ablauflinien |
|
Verbinden die Elemente und geben Anlaufrichtung vor |
|
Anweisungsteil |
|
Ein Eingang, ein Ausgang |
|
Verzweigung mit Bedingung |
|
Ein Eingang, Zwei Ausgänge, die mit JA und NEIN gekennzeichnet werden. |
Es gibt zwar noch weitere Symbole, aber mit diesen Symbolen sind Sie in der Lage die üblichen Abläufe in einem PAP darzustellen.
Beispiel eines PAPs:
Wir stellen uns folgende Situation vor. Wir sind auf einem Fest und wollen ein Bier trinken:
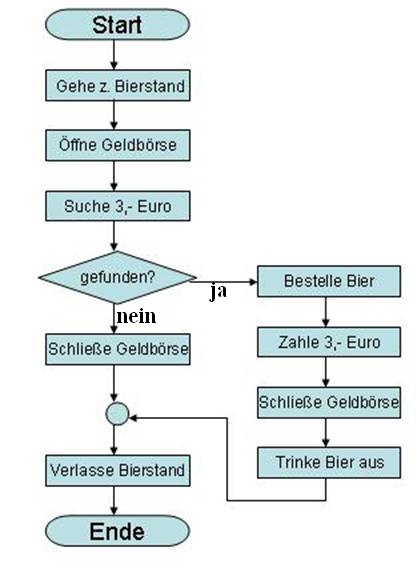
Die Vorteile des PAPs sind:
· Gute Darstellungsmöglichkeit bei einfachen Problemstellungen
· Verschiedene Abstraktionsmöglichkeiten darstellbar
· Alle wichtigen Kontrollstrukturen sind darstellbar.
Die Nachteile sind:
· Bei komplexen Problemstellungen kommt es zu einer sehr unübersichtlichen Struktur
· Für Schleifen und Rekursionen gibt es keine expliziten Darstellungselemente. Deshalb nimmt die Übersichtlichkeit signifikant ab bei der Mehrfachverwendung Schleifen und Rekursionen.
· Verzweigungen und Zusammenführungen können beliebig kombiniert werden. Das führt häufig zu einer ungünstigen Programmierung
Das die Nachteile der PAPs zu unübersichtlicher und teilweise undisziplinierter (hinsichtlich der Verwendung von Programmsprüngen) Programmierung führen, haben sich in an die strukturierte Programmierung Struktogramme als das Mittel der Wahl bei der grafischen Visualisierung durchgesetzt.
Bereits 1973 haben die Herren Nassi & Shneiderman diese Darstellungsform entwickelt. Aus diesem Grund findet man auch anstelle von PSD häufig die Bezeichnung NSD (Nassi-Shneidermann-Diagramme).
Die Elemente der Struktogramme sind aus den Kontrollelementen Sequenz, Auswahl und Wiederholung entstanden. Die Grundtypen sind recht einfach gehalten.
|
Name |
Grundtyp |
Modifikation |
|
Sequenz |
|
|
|
Wiederholung |
|
|
|
Auswahl |
|
|
Quelle der Bilder: Wikipedia (http://de.wikipedia.org/wiki/Nassi-Shneiderman-Diagramm)
Eine Sequenz stellt einen Block von Anweisungen dar. Diese werden schrittweise nacheinander (sequenziell) abgearbeitet.
Die Wiederholung stellt einen Anweisungsblock dar, der auf Grund von Bedingungen eine bestimmte Anzahl von Durchläufen ausführt. Die Überprüfung der Bedingungen findet im oben dargestellten Grundtypen am Anfang des jeweiligen Durchlaufs statt. Man spricht in diesem Fall von einer Eingangsbedingung. Die Überprüfung kann in verschiedenen Fällen auch nach dem Durchlauf sinnvoll sein. In der Modifikation ist dieses dargestellt. Man spricht nun von einer Abbruchbedingung. Die Anweisungen werden aber (im Gegensatz zum Grundtyp) in jedem Fall einmal durchlaufen.
Die Auswahl kann, wie im Grundtypen dargestellt, über zwei Möglichkeiten stattfinden (eine davon kann auch leer sein, dann haben wir eine Einfachauswahl, es wird dann im Programm weitergearbeitet. Es ist natürlich auch zulässig, die Auswahl von Möglichkeiten breiter anzulegen. Es sind mehr als zwei Möglichkeiten erlaubt (siehe Modifikation).
Diese Darstellungen sind die wichtigen Typen. Es gibt noch weitere Modifikationen, die uns aber an dieser Stelle nicht interessieren müssen.
Wichtig zu wissen ist noch, dass die Elemente der Nassi-Shneiderman Diagramme einer Norm unterliegen. (DIN 66 261).
Beispiel für eine Darstellung des Biertrinkens in einem Struktogramm nach Nassi-Shneiderman:
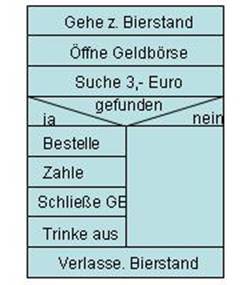
Hausaufgabe : Überlegen Sie sich einen Prozess, den Sie als PSD darstellen. Der Prozess sollte eine Schleife enthalten. (z.B. so lange mit einem Hammer auf einen Nagel schlagen, bis der Nagel in der Wand ist. Bitte senden Sie die Bilder per E-Mail an mich.
Die Vorteile des Struktogramms sind:
Die Nachteile sind:
Die Verarbeitung eines Prozesses haben wir bislang so kennen gelernt, dass es eine Aufgabe oder Aufgabekette (möglicherweise mit Unteraufgaben) gibt, der von einem Prozessor nacheinander abgearbeitet wird. Wir werden jetzt gleich sehen, dass es aber auch möglich ist, die Einzelteile des Prozesses aufzuteilen und ggf. verschiedenen Prozessoren zuzuweisen.
Nehmen wir uns den Prozess des Geschirrsäuberns nach dem Kuchenessen.
Das SADT – Diagramm würde hierfür so aussehen
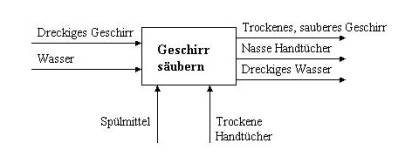
Ein Einprozessor kann auf zwei Arten das Problem lösen.
1) Zuerst alles Abwaschen danach alles Abtrocknen
Das wäre die klassische sequentielle Abarbeitung: Die erste Anweisung lautet: Abwaschen. Die zweite „Anweisung“ lautet „Abtrocknen“.
2) Ein Teil Abwaschen, danach das Teil abtrocknen dann das nächste Teil abwaschen und abtrocknen und so weiter.
Was passiert formal: Das Säubern des Geschirrs ist ein Prozess. Die Unteraufgaben Abwaschen und Abtrocknen können ebenfalls als Prozesse definiert werden, sind aber voneinander abhängig.
Wenn Wir dazu ein SADT – Diagramm zeichnen, würde dieses so aussehen:
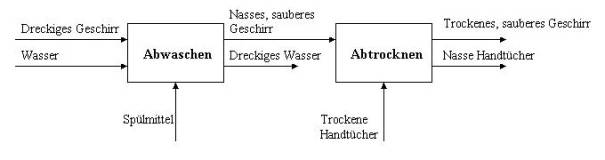
Wir haben also den Prozess des Geschirrsäuberns weiter detailliert und festgestellt, dass es zwei abhängige Prozesse gibt.
Wenn wir das Problem nun alleine (sprich als Einprozessor-System) lösen, fangen wir an, für jedes Geschirrteil zwei Arbeitsschritte zu erledigen.
Wie Sie es aus der Küche kennen, geht es schneller, wenn zwei Menschen den Abwasch machen. Einer wäscht ab und der andere trocknet ab. Wir haben in unserem alltäglichen Leben bei diesem Prozess „Geschirr säubern“ also zwei Prozessoren. Die beiden Prozessoren müssen sich aber synchronisieren, d.h. der Abtrockner muss manchmal auf ein Geschirrteil warten, da der Abwäscher (gerade bei stark verschmutzten und verkrusteten Backformen) länger für ein Teil benötigt als der Abtrockner. Dieses Warten bezeichnet man als Leerlaufzeit.
Wir haben nun gerade kennen gelernt, was parallele Verarbeitung bedeutet. Wie im richtigen Leben ist die parallele Verarbeitung von Prozessen auch in der Computertechnik zeitsparend. Bei Prozessen, die voneinander abhängig sind, spricht man von kooperierenden Prozessen. Ist ein System in der Lage, mehrere Prozesse nebeneinander zu behandeln, spricht man von Multitasking.
Nun werden Sie sagen, dass das Multitasking doch auch mit Ihrem Rechner zu Hause funktioniert. Sie haben vielleicht sogar die Hardware auseinander genommen und nur einen Prozessor gefunden. Das klingt widersprüchlich.
Es gibt auch ein Multitasking mit Einprozessor-Systemen. Allerdings passiert hier folgendes: Der Prozessor reiht die Einzelanweisungen in eine Warteschleife und macht immer abwechselnd einmal dieses und einmal jenes. Die Abarbeitung erfolgt also trotzdem sequentiell und nicht gleichzeitig. Man spricht hier von einer quasiparallelen Verarbeitung.
Echtes Multitasking mit paralleler Verarbeitung gibt es nur mit Mehrprozessor-Maschinen.