© Prof. Dr. Knut Barghorn, Jade Hochschule. Studienort WHV. E-mail: knut.barghorn@jade-hs.de
Die Turingmaschine (TM) hatten wir bereits in einem vorhergehenden Kapitel kennen gelernt und mit verschiedenen Beispielen die Arbeitsweise erklärt.
Nun soll es darum gehen, zu schauen, ob alle Algorithmen wirklich berechenbar sind, oder ob es Probleme gibt, die wir nicht mit Computern lösen können. Dazu ziehen wir wieder die Turingmaschine heran. Wir müssen diese Maschine aber zunächst etwas besser verstehen und Dann werden Wir den Algorithmusbegriff anwenden und schauen, ob jeder Algorithmus berechenbar ist oder ob es Grenzen gibt. Auch das Halteproblem wird uns hier beschäftigen. Im Zusammenhang mit diesen Fragestellungen und Begriffserläuterungen werden wir einige Beispiele, formalen Betrachtungen und fleißige Biber kennen lernen.
Sie werden in diesem Teil wieder einige Übungen und Hausaufgaben absolvieren, in denen Sie zeigen können, ob Sie das Wissen aufgenommen haben.
Wir hatten uns im Kapitel 4 bereits mit der Turingmaschine spielerisch beschäftigt. Allerdings haben wir dort den Begriff der Turingmaschine noch nicht formal behandelt. Wir werden in diesem Abschnitt sehen, dass eine Turingmaschine als Akzeptor für verschiedene Eingaben, die einer bestimmten Regel genügen, genutzt werden kann.
Zunächst wollen wir uns aber an das bereits gelernte Wissen erinnern:
Alan Turing entwickelte 1936 sein Gedankenmodell einer Maschine, auf der jede berechenbare Funktion implementiert werden kann. Dieses Modell entwickelte er beachtlicherweise bevor überhaupt reale Computer existierten.
Er trug damit entscheidend zur Präzisierung des Algorithmusbegriffs bei.
Die Leistungsfähigkeit dieser Turingmaschinen ist enorm. Jede berechenbare Funktion kann auf einer Turingmaschine implementiert werden. Es gilt auch der Umkehrschluss, dass jede Turingmaschine auch eine berechenbare Funktion darstellt.
Damit ist die Turingmaschine ebenso leistungsfähig wie moderne Hochleistungsrechner.
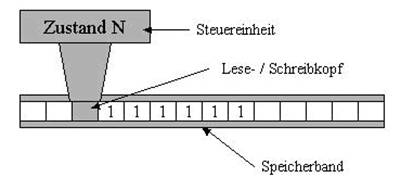
Wir hatten die Turingmaschine mit einigen Eigenschaften als Konstrukt eines endlosen Eingabebandes, einer Schreib-/Leseeinheit und einer Steuerung kennen gelernt.

Wir erinnern uns an die Aussage, dass die Maschine bei der Abarbeitung von Algorithmen verschiedene Zustände einnehmen kann. Nun ist der Begriff Zustand durch die formalisiertere Herangehensweise auch präzisiert worden, so dass wir zunächst die formale Definition einer Turingmaschine erstellen wollen.
Die Turingmaschine ist definiert als 7-Tupel:
TM= (Q, Σ, Γ, δ, q0, #, F)
Wie Sie an der Definition sehen können, wird bei der Turingmaschine klar unterschieden zwischen dem Eingabealphabet und dem Bandalphabet.
Das Bandalphabet umfasst alle Zeichen, die eine Maschine lesen und verarbeiten kann. Insbesondere ist auch das Zeichen für eine Leerstelle (Blank) im Bandalphabet neben dem Eingabealphabet enthalten. Wir hatten ja bereits gesehen, dass es bei der Sortierung von As und Bs auf unserem Band durchaus zu Leerstellen auf dem Band kommen kann.
Die Übergangsfunktion δ wird bei Turingmaschinen üblicherweise in Zustandstafeln angegeben. Jedes Paar (b, qi) (b∈B und qi ∈Q also Bandinformation, Zustand ) wird einem Tripel (b′, qi′, r) zugeordnet. Dabei sind b′∈B, qi′∈Q und r∈{L;R;H} (r steht hier für Richtung)
Die Zuordnung (b, qi)→ (b′, qi′, r) bedeutet also nichts anderes, als das, was wir bereits kennen:
Wenn sich die Turingmaschine im Zustand qi befindet und unter dem Lesekopf ein b gelesen wird, geht sie in den Zustand qi′ über, schreibt ein b′ auf das Band und rückt um einen Schritt nach r weiter (oder bleibt in der Position stehen, genau dann wenn r=H).
Um die Arbeitsweise der Turingmaschine exakt zu beschreiben, muss die Turingmaschine zunächst konfiguriert werden.
Die Konfiguration einer Turingmaschine ist nichts anderes, als dass die Turingmaschine zunächst, bevor Sie mit der Arbeit beginnt, klar positioniert werden muss, damit die Startbedingungen eindeutig sind.
Sei TM= (Q, Σ, Γ, δ, q0, #, F) eine Turingmaschine. Eine Konfiguration ist dann genau ein Augenblick, an dem die Maschine den nächsten Schritt vollziehen soll. Dieser Augenblick ist beschrieben durch den Anfangszustand und das aktuell zu lesende Zeichen. Wir können eine Konfiguration einfach ausdrücken über (a,qi). Wir müssen aber auch berücksichtigen, dass wir damit noch nicht die komplette Turingmaschine konfiguriert haben. Wir haben durchaus noch Zeichen auf dem Band links und rechts vom Schreib-/Lesekopf.
Es ist noch nicht vollständig geklärt, was die aktuelle Bandinschrift ist. Bedenken Sie, dass wir gesagt haben, das Band einer Turingmaschine sei beidseitig unendlich lang.
Die aktuelle Bandinschrift beginnt mit dem ersten Zeichenfeld, dass kein Leerfeld ist und endet
Letztlich bedeutet dies, dass ich die Konfiguration der Turingmaschine in jedem Schritt formal angeben kann als 4-Tupel:
(v,a,w,qi)
vaw ist die aktuelle Bandinschrift und qi ist der aktuelle Zustand. a drückt das Zeichen auf dem Band unter dem Schreib-/Lesekopf aus. v sind die Zeichen auf dem Band links vom Schreib-/Lesekopf und w die Zeichen rechts vom Schreib-/Lesekopf.
Wir haben also eine Anordnung in der Form dass (vawqi)∈ Γ∗ X Γ X Γ∗ X Q.
Wir nennen die Konfiguration (ε,#,w,q0) eine Anfangs- oder Initialkonfiguration bezüglich w, wenn w ein Eingabewort (w∈Σ′) ist.
Wir nennen eine Konfiguration (ε,#,v,qi) mit v∈Γ′ eine Finalkonfiguration, falls es für (ε,#,v,qi) keine Folgekonfiguration mehr gibt und qi∈F gilt. ε sei dabei eine Bandinschrift, die leer ist.
Wenn wir uns vorstellen, dass jeder Algorithmus nichts anderes ist, als die Formulierung einer Verarbeitungsvorschrift in einer formalisierten Sprache, können wir also die Turingmaschine als Akzeptor aller formalen Sprachen verstehen. Diese formalen Sprachen müssen jedoch folgender Definition genügen:
Definition: Ein Wort w wird von einer Turingmaschine TM=(Q, Σ, Γ, δ, q0, #, F)
akzeptiert, wenn die Maschine mit der Initialkonfiguration bezüglich w beginnend nach endlich vielen Schritten in einer
finalen Konfiguration stoppt.
Die akzeptierte Sprache L(TM) einer Turingmaschine in die Menge aller Worte, die von einer
TM akzeptiert werden.
Als Beispiel nehmen wir uns jetzt eine besondere Form von Worten her (eine Sprache), und schauen, ob diese von unserer TM als gültige Worte akzeptiert werden.
Die Sprache soll alle Worte umfassen, die nach der Regel anbncn mit n ∈ N gebildet werden.
Daraus entstehen dann die Worte abc, aabbcc, aaabbbccc, ....
Also immer gleich viele as,bs und cs in geordneter Reihenfolge.
Nun brauchen wir eine TM, die genau alle Worte dieser Sprache akzeptiert. Das folgende Beispiel zeigt diese TM.
Beispiel:
Wir definieren uns folgende TM=(Q, Σ, Γ, δ, q0, #, F) mit:
| Zustand / Eingabe | |||||||
| - | - | - | - | - | - | (q1,#,R) | |
| (q2,0,R) | - | - | - | (q5,1,R) | - | - | |
| (q2,a,R) | (q3,1,R) | - | - | (q2,1,R) | - | - | |
| - | (q3,b,R) | (q4,2,L) | - | - | (q3,2,R) | - | |
| (q4,a,L) | (q4,b,L) | - | (q1,0,R) | (q4,1,L) | (q4,2,L) | - | |
| - | - | - | - | (q5,1,R) | (q5,2,R) | (q6,#,L) | |
| - | - | - | (q6,0,L) | (q6,1,L) | (q6,2,L) | (q6,#,H) |
Sehen wir uns nun anhand der Konfigurationsfolge an, wie der Algorithmus für die Akzeptanzprüfung auf das Wort w=abc abgearbeitet werden kann.
(ε, #, abc, q0) ⇒
(#, a, bc, q1) ⇒
(#0, b, c, q2) ⇒
(#01, c, ε, q3) ⇒
(#0, 1, 2, q4) ⇒
(#, 0, 12, q4) ⇒
(#0, 1, 2, q1) ⇒
(#01, 2, ε, q5) ⇒
(#012, #, ε, q5) ⇒
(#01, 2, ε, q6) ⇒
(#0, 1, 2, q6) ⇒
(#, 0, 12, q6) ⇒
(ε, #, 012, q6) ⇒
STOP
Damit haben wir gezeigt, dass es eine finale Konfiguration für das Eingabewort abc gibt.
Wir haben an dieser Stelle auch gesehen, dass es möglich ist, dass wir eine Turingmaschine für eine Sprache realisieren können, die nicht als kontextfreie Sprache klassifiziert werden konnte.
Wir wollen nun noch ein Gegenbeispiel probieren. Mit der obigen TM werden wir versuchen, das Wort ab zu parsen.
Wir sehen uns wieder die Konfigurationsfolge an:
(ε, #, ab, q0) ⇒
(#, a, b, q1) ⇒
(#0, b, ε, q2) ⇒
(#01, #, ε, q3) ⇒
STOP, da δ(#, q3) nicht definiert ist.
Da q3 kein Endzustand ist (q3∉F) wird das Eingabewort ab von dieser TM nicht akzeptiert.
Ein weiteres Beispiel zeigt, dass die Turingmaschinen auch andere Sprachen akzeptieren können.
Beispiel:
Wir nehmen dazu eine Sprache, die aus den beiden Elementen a und b besteht. Die Voraussetzung soll sein, dass die Wort der akzeptierten Sprache mindestens zwei a enthalten.
Die Turingsmaschine wird wie folgt beschrieben:
| Zustand / Eingabe | |||
| - | - | (q1,#,R) | |
| (q2,a,R) | (q1,b,R) | - | |
| (q3,a,L) | (q2,b,R) | - | |
| (q3,a,L) | (q3,b,L) | (q3,#,H) |
Die Turingmaschine hat bei dieser Aufgabe eine rein lesende Funktion.
Nun erinnern wir uns aber wieder daran, dass wir mit der Turingmaschine gestartet waren, um den Algorithmusbegriff klarer definieren zu können. Dabei ging es vornehmlich um den Begriff Berechenbarkeit. Wenn es eine Definition gibt, in der dieser Begriff die Algorithmendefinition einengt, dann ist zu erwarten, dass es Berechnungsvorschriften gibt, die nicht berechenbar sind. Damit gibt es demnach auch keine Turingmaschinen die diese Vorschriften darstellt und der Bedingung des "Stoppens" genügt.
Dieser Problematik werden wir uns nun annehmen. Insbesondere die beiden Begriffe "Berechenbarkeit" und "Stoppen" werden wir uns im Folgenden näher ansehen.
Zunächst werden wir uns klar machen, dass es Funktionen gibt, die nicht berechnet werden können.
Wir wissen, dass wir jede Menge von Objekten, die wir aufzählen können, genauso groß ist, wie die Menge der natürlichen Zahlen. Diese Aussage stammt von einem deutschen Mathematiker namens Georg Cantor (1845-1918). Das gilt auch für Turingmaschinen, wie wir gleich sehen werden.
Wir können jede Turingmaschine durch eine Zeichenkette endlicher Länge beschreiben. Das fordert auch die Definition der Turingmaschine.
Das bedeutet, dass alle Turingmaschinen und damit auch berechenbaren Funktionen aufzählbar sind.
Nehmen wir und dazu eine Zeichenkette mit der Länge 1 her. Die erlaubten Zeichenmenge möge insgesamt 40 Zeichen (lässt sich gut rechnen) enthalten. (26 Buchstaben, 10 Ziffern und 4 Sonderzeichen).
Bei der Länge von einem Zeichen habe ich also 40 verschiedene Kombinationen.
Bei einer Länge der Zeichenkette von maximal 2 Zeichen habe ich nun die ersten 40 Kombinationen und zusätzlich 402 Zeichenkombinationen für die zweistellen Ketten.
Bei einer maximalen Länge von N Zeichen habe ich nun die NN verschiedenen Ketten der festen Länge N und dazu die NN-1 Kombinationen der Kette mit der Länge N-1 Zeichen und so weiter bis zu den einstellen Ketten mit N verschiedenen Kombinationen.
Insgesamt habe ich also NN + NN-1 + ...... + N2 + N verschiedene Turingmaschinen.
Die Anzahl der Turingmaschinen ist damit zwar unendlich, aber abzählbar. Die Menge der natürlichen Zahlen ist ebenfalls abzählbar. Damit sehen wir, dass die Menge des Turingmaschinen und der natürlichen Zahlen gleich groß (besser: gleich mächtig) sind.
Wie sieht es nun mit der Menge aller Funktionen aus?
Wenn auch diese abzählbar sind, habe ich für jede Funktion eine zuordenbare Turingmaschine und jede Funktion ist berechenbar.
Wenn wir eine Menge von Funktionen hernehmen, die natürliche Zahlen in den Zahlenraum der ganzen Zahlen abbilden,
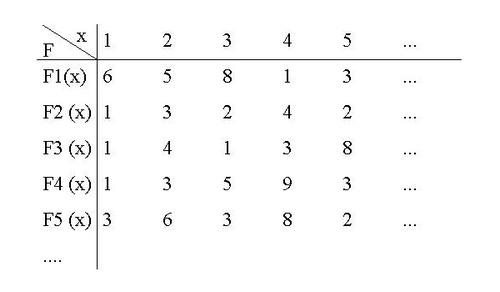
dann kann ich für jede Funktion eine Zahl N finden, die die Funktion eindeutig bestimmt.
Wenn ich nun aber die Cantorsche Diagonalisierung anwende, werden wir sehen, dass die Menge dieser Funktionen überabzählbar ist.
Dazu wähle ich eine Funktion, die nicht in der Liste steht. Da funktioniert wir folgt. Ich definiere, dass ich einen Funktionswert 1 meiner Funktion F1(x) finden kann, der nicht dem Funktionswert in der Liste entspricht und setze ihn für Fneu(1) ein. Gleiches mache ich bei dem zweiten Funktionswert der zweiten Funktion F2(x) und so weiter, bis zum n-ten Funktionswert der Funktion Fn(x).
Damit habe ich eine neue Funktion, die nicht in der Liste steht. Die neue Funktion unterscheidet sich immer in genau einem Funktionswert von den gelisteten Funktionen.
Damit haben wir gezeigt, dass die Menge der Funktionen überabzählbar ist.
Das Problem ist nun, dass ich überabzählbar viele Funktionen dieser Art habe und nur abzählbar viele Turingmaschinen. Mindestens eine dieser Funktionen lässt sich also auf einer Turingmaschine nicht abbilden.
Die Suche von Cantor und anderen nach einer nicht berechenbaren Funktion dieser Art ist bislang nicht von Erfolg gekrönt, aber wir werden gleich noch ein Beispiel für eine nicht berechenbare Funktion kennenlernen.
Wir werden nun den Begriff Berechenbarkeit formalisieren und eine Definition dafür aufstellen.
Gegeben sei eine TM, und eine Funktion f: A1 → A2. Weiterhin sei ein Eingabealphabet Σ und Worte w über Σ gegeben.
Eine Funktion f heißt Turing-berechenbar, wenn es eine Turingmaschine gibt, die f berechnet.
Die TM berechnet f: f: A1 → A2, wenn für alle w ∈ A1 gilt: (ε, #, f(w), q0) geht nach endlich vielen Schritten in (ε, #, f(w), q) über, wobei (ε, #, f(w), q) eine Finalkonfiguration ist.
und
für w ∉ A1 geht die TM nie in eine Finalkonfiguration über.
Um dieses besser verstehen zu können, gebe ich Ihnen einige Beispiele an die Hand.
Wir können uns schnell klarmachen, dass die Funktion f(n)=n+1 Turing-berechenbar ist. Wir stellen die natürlichen Zahlen anhand von der zugehörigen Anzahl aufeinander folgender Striche auf dem Band dar. Die Turingmaschine muss nun lediglich einen weiteren Strich hinzufügen.
Wir haben in einem früheren Kapitel gesehen, dass die Funktion f(n,m)=n+m Turing-berechenbar ist. Dabei hatten wir die natürlichen Zahlen als aufeinander folgenden Einsen dargestellt. Wir mussten nur die Rechenzeichen ersetzen.
Wie wir bereits oben gesehen haben, hat die Berechenbarkeit Grenzen. Um ein Beispiel zu sehen, wo diese Grenzen liegen, sehen wir uns das Beispiel der Fleißigen Biber an.
Der ungarische Mathematiker T. Rado ersann 1962 ein Spiel, um seinen Studenten das Problem der Berechenbarkeit nahe zu bringen. Dabei geht es um Folgendes:
Es ist eine beidseitig unendliche Turingmaschine mit n Zuständen {q0, q1, ... qn} sowie einem Haltezustand und ein zweiwertiges Bandalphabet {|, #} gegeben.
Die Turingmaschine soll bei jedem Schritt ein Symbol schreiben und grundsätzlich eine Bewegung nach links oder rechts machen oder anhalten. Die Idee ist nun, eine Berechnungsvorschrift zu finden, die bei festen n angesetzt auf ein zunächst leeres Band die meisten Striche auf das Band schreibt. Es ist erlaubt, zwischen den Strichen auch Leerstellen (Lücken) zu erzeugen.
Die Maschine, die mit n Zuständen und ihrer Berechnungsvorschrift die meisten Striche erzeugt erhält den Titel "Fleißigster Biber".
Die Funktion, die diese Maschine berechnet nennt man nach Ihrem Erfinder Rado-Funktion.
Korrekt angegeben lautet die Rado-Funktion (bb steht für busy beaver): bb: N → N, n → bb(n)
bb(n) ist dabei die Anzahl der Striche auf dem Band.
Für eine Maschine mit genau einem Zustand n=1 (q0) ist das Problem trivial. Bedenken Sie aber, dass die Maschine auch anhalten muss. Ansonsten wäre es einfach, mit genau einem Zustand unendlich viele Striche zu erzeugen.
Aufgabe zum Mitdenken: Wie kann die Vorschrift aussehen, um mit einer Maschine mit einem Zustand einen Strich zu erzeugen?
Bei zwei Zuständen (q0, q1) ist die Vorschrift ebenfalls noch recht einfach.
Wir überlegen uns hierzu folgenden Algorithmus:
Der mit dieser TM erzeugte Bandinhalt weist immerhin 4 Striche auf.
Aufgabe: Versuchen Sie einen Biber mit drei Zuständen zu erzeugen. Ich verrate Ihnen, dass es lange gedauert hat, bis jemand einen Algorithmus gefunden hatte, mit dem in 13 Schritten 6 Striche erzeugt werden können.
Rado selbst war in Zusammenarbeit mit Shen Lie der Erfinder dieser n=3 TM, die 6 Striche erzeugte.
Für das Problem n=4 dauerte es bis 1972 bis Weimann zeigen konnte, dass sein Biber 4. Ordnung mit 13 Strichen der bestmögliche Biber war.
Man dachte, dass man jetzt auch sehr schnell Biber finden würde für n=5. Man erwartete, dass die Anzahl der Striche sich im Rahmen einer Reihe (1,4,6,13) entwickeln würde. Allerdings stellte sich das Problem als weitaus schwieriger heraus.
Es muss nämlich auch gezeigt werden, dass es keinen Biber gibt der fleißiger ist. D.h. es müssen alle anderen Zuweisungskombinationen ausprobiert werden. Dabei müssen dann auch die Biber, die zwar eine Menge Striche erzeugen, aber nicht anhalten aussortiert werden.
Man entwickelte Programme, die (in etwa) folgende Arbeitsweise hatten:
Es kam aber anders als erwartet. Sehr bald wurden Biber gesichtet, die mehr als 100 Striche erzeugten. Diesen großen Sprung für die erzeugten Striche von n=4 auf n=5 hatte keiner erwartet.
Im Jahr 1983 veröffentlichte Schult einen n=5-Biber, der 501 Striche erzeugte. 1984 kam Ushing daher und präsentierte einen Biber der 1915 Striche erzeugt. Einen neuen Rekord stellte der Spezialist für fleißige Biber Heiner Marxen gemeinsam mit Jürgen Buntrock auf. Sie stellten eine n=5-Maschine vor, die in mehr als 47 Mio. Schritten 4098 Striche erzeugt. Bislang ist das der Rekord.
Auch die Suche nach einem fleißigen Biber 6. Ordnung wurde von Heiner Marxen angegangen. Er fand einen Biber, der 1,29x10865 Striche erzeugt. Allerdings benötigt der Biber auch mehr als 3x101730 Schritte.
Die folgende Tabelle zeigt Ihnen, wie weit die Menschen bislang gekommen sind:
| Anzahl der Zustände | Maximale Schritte | Maximal erzeugte Einsen |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 6 | 4 |
| 3 | 21 | 6 |
| 4 | 107 | 13 |
| 5 | ≥ 47,176,870 | ≥ 4098 |
| 6 | ≥ 3x101730 | ≥ 1,29x10865 |
| 7 | Abschätzung nicht möglich | Abschätzung nicht möglich |
Es gibt auch eine Menge Varianten, die ich hier der Belustigung wegen nennen möchte.
So wurden beispielsweise Biber entwickelt, die keine Striche (nicht mal einen) erzeugen, sondern einfach verschiedene Überlebensstrategien nachempfinden:
Sie sehen, mit Bibern lässt sich prima spielen.
Um auch Ihnen die Möglichkeit zu geben, fleißige oder andere Biber zu erzeugen, hier einige Links, die auf Java-Applets verweisen, die Turingmaschinen für fleißige Biber simulieren. Als ersten Link finden Sie die Seite von dem deutschen Biber-Spezialisten Heiner Marxen.
Warum kann aber nun nicht berechnet werden, wie sich diese Maschinen verhalten?
Diese Frage werden wir nun versuchen zu klären. In diesem Zusammenhang treten aber noch andere Fragen auf, die es auch noch zu erläutern gilt:
Die obigen Fragen beziehen sich genau auf diese drei Themen. Zunächst werden wir die Fragestellung der Berechenbarkeit angehen.
Man war lange der Meinung, dass jede Aussage algorithmisch entscheidbar ist, d.h. man glaubte, dass man jeder Aussage algorithmisch zuordnen könne, ob sie lösbar oder nicht lösbar sei. Die beiden Mathematiker Hilbert (der, nach dem der Hilbert-Raum (Erweiterung des Euklidischen Raums auf unendlich viele Dimensionen) benannt wurde und Gödel (einem der führenden Logiker des letzen Jahrhunderts, der sich besonders um dieses Problem verdient gemacht hat) stritten sich jahrelang darüber, bis Gödel 1931 die Lösung (das Unvollständigkeitstheorem) veröffentlichte. In diesem Theorem legt er dar, dass es nicht möglich ist, jede Aussage algorithmisch zu überprüfen. Damit zeigte er letztlich auch, dass nicht alle Probleme durch Computer gelöst werden können.
Um zu beweisen, dass jedes Problem algorithmisch entscheidbar oder nicht entscheidbar ist, muss man zunächst den Begriff Algorithmus formalisieren. Wir haben gesehen, dass dies über die Turing-Maschine gelungen ist. Wenn wir uns nun wieder ins Gedächtnis rufen, dass die Turingmaschine als abstrakte Beschreibung eines Computers gelten kann.
Wir haben auch gesehen, dass die Darstellung eines Algorithmus in Form einer Turingmaschine nichts anderes ist, als die Formulierung desselben Problems in einer formalen Sprache.
Die Entscheidbarkeit wird in einer von Alonzo Church und Alan Turing formulierten These, die bislang keiner widerlegen konnte und daher als allgemein akzeptiert gilt formuliert:
Eine Funktion ist genau dann Turing berechenbar, wenn Sie intuitiv berechenbar ist.
Was aber heißt nun eigentlich intuitiv berechenbar? Letztlich versteht man darunter alle Funktionen, die prinzipiell auch von einem Menschen ausgerechnet werden könnten.
Wenn man dieses etwas "griffiger" formulieren möchte, kann man auch sagen:
Eine Funktion f(x) heißt berechenbar, wenn es einen Algorithmus gibt, der bei gegebenen x das Ergebnis f(x) liefert.
alternativ kann man formulieren:
Ist eine Menge M gegeben, so heißt M entscheidbar, wenn es einen Algorithmus gibt, der für jedes vorgegebene Element x die Aussage liefert, ob x in M enthalten ist oder nicht.
Diese Aussagen haben aber alle die Annahme, dass es Funktionen gibt, die nicht berechenbar oder Entscheidbar sind. Diese Annahme können wir uns aber schnell klarmachen.
Wir wissen bereits, dass die Menge der Algorithmen abzählbar ist. Dies lässt sich einfach dadurch herleiten, dass die Menge des Eingabealphabetes A endlich ist. Dazu kommt dann noch, dass auch die Menge der Zustände endlich ist.
Die Menge der Worte, die sich aus einem Alphabet Σ bilden lassen, ist zwar unendlich, aber immer noch abzählbar.
Daraus resultiert, dass auch die Menge der möglichen Turingmaschinen und damit die Menge der Algorithmen abzählbar ist (wir könnten also die Turingmaschinen "durchnummerieren".)
Die Menge der möglichen Funktionen ist aber (wie auch die Menge der Reellen Zahlen) überabzählbar.
Demnach muss es also Funktionen geben, die nicht berechenbar sind. Wir werden dies nun an einem Beispiel sehen.
Das Halteproblem
Wir können relativ schnell zeigen, dass eine Maschine nicht erkennen kann, ob sie terminiert oder nicht.
Das lässt sich durch einen Widerspruchsbeweis eindeutig zeigen. Die Beweisidee kann man gut im Pseudocode darstellen:
Da wir den Beweis durch Widerspruch lösen wollen setzen wir an, dass es eine Funktion gibt, die die Terminiertheit überprüft. Wir nennen diese Funktion stopptest.
stopptest(Programm, Eingabe)
wenn Programm(Eingabe) terminiert
dann return Ja
sonst return Nein
Diese Funktion setzen wir nun im Programm test ein:
test(Programm)
solange stopptest(Programm, Programm) == Ja
führe aus keine Aktion
Diesem Programm geben wir nun sich selbst als Eingabedaten und prüfen sie damit von der Methode stopptest auf Terminierung, dann kann diese kein richtiges Ergebnis liefern:
test(test); //Dieser Aufruf terminiert genau dann,
// wenn er nicht terminiert. (Widerspruch!)
Das bedeutet, es kann keine Turingmaschine geben, die, wenn sie als Eingabe die Codierung einer Turingmaschine TM und eine zugehörige Eingabe w erhält , Ja ausgibt, wenn TM auf w hält und Nein ausgibt, wenn TM nicht auf w hält.
Das Halteproblem kann also nicht entschieden werden. Damit steht die Programmentwickler- und Anwendergemeinde vor dem Problem, dass niemals klar gesagt werden kann, ob ein Programm noch irgendwann terminiert oder nicht. Bei unserem Beispiel mit den fleißigen Biber bedeutet dies, dass Sie wirklich alle !!! möglichen Turingmaschinen ausprobieren müssen, da auch die Rado-Funktion zu den nicht berechenbaren Funktionen gehört.
Um klar zu machen, was das bedeutet, kann man sich vor Augen führen, welche Anzahl von Turingmaschinen für ein festes n sie ausprobieren müssen (und dabei nie wissen, wie viele Schritte bis zur Terminierung nötig sind, sofern die Maschine überhaupt terminiert).
Wir haben eine Turingmaschine mit n-Zuständen sowie einem zweiwertigen Bandalphabet.
Das bedeutet, unsere Turingtafel, die die Übergänge enthält, hat exakt 2n Einträge.
Jeder Eintrag in der Turingtafel enthält ein Tripel (neuer Zustand, zu schreibendes Zeichen, Bewegungsrechtung)
Das bedeutet, jeder Eintrag kann (n+1)*2*2 Möglichkeiten der Kombination besitzen.
Für die Biber heißt dies, dass wir 4(n+1)2n verschiedene Turingtafeln und damit verschiedene Turingmaschinen haben.
Damit haben wir folgende Tabelle, die uns zeigt, dass die Anzahl der zu überprüfenden Maschinen bei steigendem n sehr schnell wächst.
| n | Anzahl der Maschinen | bb(n) |
| 1 | 16 | 1 |
| 2 | 20736 | 4 |
| 3 | 1,6*107 | 6 |
| 4 | 2,6*1010 | 13 |
| 5 | 6,3*1013 | ≥ 4098 |
| 6 | 2,5*1017 | ≥ 1,29*10865 |
| 7 | 1,18*1021 | ? |
Damit können Sie sich vorstellen, dass es sehr schwierig sein wird, für einen n≥7 -Biber die optimale Lösung herauszubekommen. Die Suche nach dem fleissigsten Biber für 5 Zustände hat mehrere Tage Rechenzeit auf einem Supercomputer verschlungen. Ihnen bleibt nun das Probieren und Sie müssen ziemliches Glück haben, wenn Sie in Ihrem Leben den Titel "bester Biber-Sucher" erringen wollen.
Wir haben nun gesehen, dass es eine Reihe von Problemen geben muss und gibt, die nicht berechenbar sind.
Bereits bei der Definition von Algorithmen nach Kübe haben wir gesehen, dass ein Algorithmus auch über die Effizienz definiert wird.
Die Effizienz sagt aus, dass möglichst wenig Rechnerressourcen verbraucht werden sollen. Zwar ist bei einer Simulation mit einer Turingmaschine, die über ein unendliches Speicherband verfügt, die Speicherkapazität nicht beschränkt, aber in der Realität ist bei einem Computer der Speicherplatz endlich.
Wenn wir einen Algorithmus auf einem Computer implementieren wollen, haben wir also auch die Aufgabe, zu schauen, ob der endliche Speicherbedarf ausreicht.
Des Weiteren haben wir ein Zeitproblem. Wir wollen unseren Algorithmus ja auch in endlicher Zeit ablaufen lassen. Diese ist zwar immer dann gegeben, wenn der Algorithmus terminiert. Es bleibt aber die Frage danach, wann der Algorithmus voraussichtlich beendet sein wird.
Die beiden wesentlichen Parameter für die Komplexitätsbestimmung sind also:
Wie lassen sich diese Komplexitäten abschätzen. Dazu sehen wir uns einfache Beispiele an:
Beispiel: Skalarprodukt Wir nehmen das Skalarprodukt zweier Vektoren x=(x1, x2, ..., xn) und y=(y1, y2, ..., yn).
Zur Erinnerung: Das Skalarprodukt ist definiert als Summe der Einzelprodukte gleicher Indizes.
x1 * y1 + x2 * y2 + .... + xn * yn
Bei einer Dimension n haben wir also
T(n) = n für die Multiplikation
T(n) = n-1 für die Addition der Produkte
Insgesamt werden wir also n+n-1 Rechenoperationen durchführen müssen, um das Problem zu lösen.
Bei einer Komplexitätsbetrachtung sind wir aber nicht so sehr daran interessiert, genau zu wissen, wie viele Operationen notwendig sind, sondern es interessiert uns vielmehr das Verhalten für große n.
Um dafür eine grobe Abschätzung zu bekommen, reicht es völlig aus, wenn wir uns auf den Term beschränken, der das größte Wachstum aufweist.
Für das Problem Skalarprodukt können wir aussagen, dass es die Komplexität linearer Ordnung hat. T(n)=O(n)
Beispiel: Polynom Bei der Auswertung eines Polynoms haben wir sogar zunächst eine höhere Komplexität, wie wir gleich sehen werden.
p(x) = an xn + an-1 xn-1 + ....+ a1 x + a0
Aufgabe:Wie viele Operationen müssen Sie für Polynome mit n=2, n=3, n=4 und n=10 durchführen?
Aus der obigen Aufgabe erkennen Sie, dass die Anzahl der Operationen nicht linear, sondern schneller wächst.
Die Anzahl der Additionen ist linear wachsend mit n. Aber bei den Multiplikationen stellen wir fest, dass diese bei steigendem n stark zunehmen.
Mathematisch ist das Wachstum beschreibbar durch:
AnzahlMult. = 0 + 1 + 2 + .... + n-1 + n = n(n+1)/2 oder anders ausgedrückt: = n2/2 + n/2.
Wir sehen also, dass die Berechnung von Polynomen ein Problem mit einer Komplexität quadratischer Ordnung ist.
Für sehr groß werdenden n ist die Polynomberechnung also eine zeitfressende Operation. Glücklicherweise hat allerdings Herr Horner schon im Jahre 1819 ein Schema entwickelt, das Problem etwas anders zu lösen, um die Komplexität in den Griff zu bekommen. (Es soll auch schon einem Chinesen 500 Jahre zuvor gelungen sein, aber der Preis der Ehre ging an William G. Horner)
Das Horner Schema ist recht einfach zu verstehen. Durch eine andere Schreibweise wird das Polynom "rechnerfreundlicher" ausgedrückt.
p(x)= ((..(an x + an-1) x + ....+ a
In einem Beispiel von n=3 ist das Horner-Schema noch übersichtlich darstellbar:
p(x)=((a3 x + a2) x + a1) x + a0
Wenn Sie in dieser Schreibweise die Anzahlen der Additionen und Multiplikationen ermitteln, werden Sie feststellen, dass genau n Additionen und n Multiplikationen nötig sind.
Damit ist es gelungen, die Komplexität von Polynomberechnungen deutlich zu senken.
Neben den beiden Komplexitätsklassen, die wir gerade kennen gelernt haben (linear und polynomial), gibt es auch noch weitere Ordnungen. Man unterscheidet in erster Linie die Klassen logarithmische Ordnung und die Ordnungen 2n und nn.
Welche Komplexität in diesen Klassen wirklich verborgen ist, sieht man schön an der folgenden Tabelle:
| Anzahl Eingabedaten [n] | ||||||
Um uns die Bedeutung dieser Zahlen klar zu machen, sagen wir einfach, dass wir für die Operation einen sehr schnellen Rechner zur Verfügung haben. Wir gehen davon aus, dass er 1 Billionen Operationen (1012)pro Sekunde schafft. (Zur Erinnerung: 1970 schafften die Rechner der vierten Generation gerade mal 10 Millionen Operationen pro Sekunde. Die heutigen Rechner sind mit Taktraten von unter 5 GHz ausgestattet. Nehmen wir freundlicherweise mal an, die Rechner seien in der Lage je Takt eine Operation auszuführen, dann erhalten wir eben bei 5 GHz-Rechnern 5*109 Operationen pro Sekunde)
Dieses sei uns aber zu langsam und wir bleiben mal zukunftssicher und nehmen 1012 Operationen pro Sekunde an.
Eine Operation dauert demnach also eine Picosekunde (10-12s). Wenn wir nun ein Problem mit der Komplexitätsordnung 2n vorliegen haben mit 100 Eingaben, werden 1030 Operationen benötigt. Wenn wir die Zeiten hernehmen, ergibt sich auf unserem Supercomputer ein Zeitbedarf von 1018 Sekunden. Das sind immerhin 1,6*1016 Minuten oder 2,7 *1014 Stunden. Das wiederum sind 2,3 *1013 Tage oder 6,3 *1010 Jahre.
Wir landen damit ziemlich genau bei dem Wert, der augenblicklich als geschätztes Alter des Universums angegeben wird.
Beispiele für zu komplexe Probleme
Nun werden Sie sicherlich fragen, welche Probleme denn eigentlich in die Klasse der nicht berechenbaren Probleme fallen. Dazu gebe ich Ihnen nun noch ein Beispiel:
Sie wollen alle Primzahlen im Bereich 0-n bestimmen.
Es gibt einen guten Algorithmus dafür, den schon die alten Griechen kannten und der sich schön auf einem Computer implementieren lässt.
Zunächst nochmal: Was genau ist eine Primzahl. Eine Zahl, die ohne Rest nur durch genau zwei Zahlen (sich selbst und die 1) teilbar ist.
Wenn n keine Primzahl ist, dann gibt es immer einen größten Teiler k, für den gilt, dass er kleiner oder gleich der Wurzel aus n ist.
Der Algorithmus heißt Sieb des Eratosthenes und funktioniert folgendermaßen:
Es wird eine Tabelle aufgestellt mit allen ungeraden Zahlen von 3 bis n.
Wir setzen nun p=3 und streichen aus der Tabelle alle Zahlen, die ein Vielfaches (v) von p darstellen.
Nach dem kompletten Durchlauf von p=3 setzen wir p gleich der niedrigsten verbliebenen Zahl und lassen es wiederlaufen. So fahren wir wir also nacheinander mit p=5, p=7 und p=11 usw. fort.
Der Algorithmus ist dann beendet, wenn p ≥ Wurzel aus n ist.
Alle verbliebenen Zahlen in der Tabelle sind nun definitiv Primzahlen.
Versuchen wir einmal die Komplexität diese Algorithmus` abzuschätzen. Wir suchen also nach den wesentlichen Operationen dieses Verfahrens. Ein wesentlicher Vorgang ist das Streichen der Zahlen aus der Tabelle. Dazu müssen die Operationen der Multiplikation von p durchgeführt werden. Um die zu löschenden Werte zu ermitteln sind 10n/2 Operationen notwendig. Das bedeutet, hier haben wir einen Algorithmus, der für große n nicht mehr berechenbar ist, obwohl es einen Algorithmus dafür gibt, der sich sogar auf Computern implementieren lässt.
Gerade wenn es um das Thema Sicherheit geht, werden vielen Menschen empfindlich. Aus diesem Grund hat man angefangen, Daten verschlüsselt zu übertragen.
Die ersten Verschlüsselungen nutzten weniger als 56 Bit (DES=56Bit). Bei dieser Schlüssellänge sind 256 = 7,2 * 1016 verschiedene Möglichkeiten enthalten.
Raffinierte Methoden kennen wir nicht, um so einen Code zu knacken, Raten wäre eher sinnlos. Die Wahrscheinlichkeit richtig zu liegen, liegt etwa so hoch, wie im Lotto zu gewinnen und gleichzeitig vom Blitz erschlagen zu werden.
Wir probieren also alle Codes nacheinander aus. Brute Force!
Stellen Sie sich vor wir hatten vorher doch noch etwas Glück und gewannen tatsächlich im Lotto und ließen uns tausend moderne Computer bauen. Diese Computer können 5.000.000.000 (5 Milliarden) Schlüssel pro Sekunde berechnen. So, jetzt denken wir uns noch ein ausgeklügeltes System aus, so dass wir jeden Computer effektiv nutzen können. Wir verbinden unsere 1.000 Computer zu einem Computer, der jetzt 1.000 · 5.000.000.000 Schlüssel pro Sekunde berechnen kann. Wir teilen 7,2 · 1016 also durch 5 Billion und erhalten die Zeit in Sekunden, die wir brauchen, um DES zu knacken: 14.411 s. In Stunden sind das (geteilt durch 3.600) 4 Stunden.
Stellen wir uns vor, wir seien eine Regierung (mit einem einigermaßen guten Etat). Wir kaufen 1 Million CPUs (Wert: unter 200 Mio. Euro) , die jeweils 5 Milliarden Schlüssel pro Sekunde berechnen können. Damit ergeben sich 14,4 s zum Knacken von DES!
Der Schlüssel ist also Berechenbar, die Komplexität zu gering
Bei 128-Bit (das ist lediglich ein größeres n in unserer Komplexität 2n).
Es ergeben sich nun hier eine bessere (für die Sicherheit) Rechnung:
2128 = ca. 1038. Wir probieren wieder die Rechnung mit tausend CPUs, die 5 Milliarde Schlüssel pro Sekunde berechnen können.
Wir rechnen 1038 / 1.000 / 5.000.000.000 / 3.600 / 24 / 365 und erhalten somit 6 *1017 Jahre. (Zum Vergleich, die Sonne wird in etwa 5 * 109 Jahren verglühen. Es darf also als unwahrscheinlich angenommen werden, dass dann noch Menschen aus das Ergebnis der Rechnung warten.
Versuchen wir es als superreiche Regierung, denen eine verschlüsselte Nachricht 1012 (eine Billion) Euro wert ist. Sie würde 5 Milliarden CPUs kaufen. Diese Regierung würde den DES-Schlüssel in weit weniger als 1 Sekunde knacken.
Für den 128-Bit Schlüssel benötigt sie nun aber: 1038 / 5*109 / 5*109 / 3600 / 24 / 365 ungefähr 125 Milliarden Jahre.
Satz 1:
Führt man berechenbare (ausführbare) Algorithmen nacheinander aus, so ist der neue gesamte Algorithmus ebenfalls berechenbar (ausführbar)
Satz 2:
Ersetzt man Einzelschritte in einem ausführbaren Algorithmus durch ausführbare Algorithmen, ist der neue Algorithmus ebenfalls ausführbar
Echte Hausaufgabe: Warum ist es bis heute niemandem gelungen, zu widerlegen, dass jede Zahl eine wundersame Zahl ist, oder zu beweisen, dass jede Zahl wundersam ist? Erläuterung: Eine Zahl ist dann wundersam, wenn sie mittels folgenden Algorithmus auf eins zurückgeführt werden kann: ist n gerade, teile n durch 2 und setze das Ergebnis gleich n. Ist n ungerade, multipliziere n mit drei, addiere eins und setze das Ergebnis gleich n.